Sectieoverzicht
-
In this course you will learn about:
- Expanding brackets.
- Factorising by grouping.
- Factorising by finding the difference of two squares.
- Factorising trinomials.
- Simplifying algebraic fractions.
-
Remember that a product is the result of multiplication. When you multiply brackets that contain terms you end up with algebraic expressions.
Make sure you understand all of the concepts taught in Form I Algebra before you start with this course.
Try this activity to check your skills of multiplying a monomial by a binomial.-
FOIL
When we multiply two linear binomials, we can use the word FOIL (First Outers Inners Last) to help us remember that each term in the first bracket must be multiplied by each term in the second bracket.
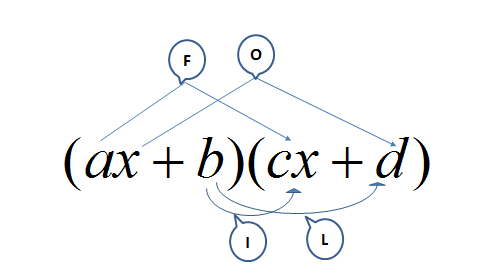
It is important to understand FOIL as you will come back to this concept in factorisation. Watch the video Multiplying binomials to learn more about FOIL.
-
Factorisation reverses the process of multiplying and expanding brackets.
For example, if we expand \(3(a+2)\) we get \(3a+6\). When we factorise, we start with \(3a+6\) and end up with \(3(a+2)\). The two expressions are exactly the same in value no matter what values we substitute for \(a\).
Finding the Highest Common Factor (HCF) is just one of the ways that we factorise expressions. A common bracket can be taken out as an HCF if the bracket is identical in all terms, we call this factorising by taking out the highest common bracket or grouping.
Factorising by taking out the highest common bracket is discussed in more detail in the following video. Make sure you try the activity that follows the video to test your knowledge of grouping.
-
A difference of two squares is a perfect square subtracted from another perfect square. A difference of squares can be rewritten as a product of binomials containing the same terms but opposite signs because the middle terms will cancel each other out if the two factors are multiplied.
For example, \(9-4\) is a difference of two squares. \(9=3\times3\) and \(4=2\times2\) and the terms are separated by a "\(-\)" sign. So, we can rewrite \(9-4\) as \((3-2)(3+2)\). You can check for yourself that this is true, \(9-4=5\) and \((3-2)(3+2)=5\).
This concept can be explained using the areas of squares as shown in the next animation of difference of two squares.
-
How to factorise the difference of two squares
To use the difference of two squares to factorise you must check that the expression contains two perfect squares and a minus sign.
The next video shows examples of difference of two squares, which you must understand before trying the next activity.
-
Practise finding the difference of squares
Click on the link to the exercise to practise your skills. Difference of squares.
-
-
A quadratic expression is any expression where the variable has a highest power (or degree) of two. \(a{x}^{2}+bx, {x}^{2}, {a}^{2}-{b}^{2}\) and \(a{x}^{2}+bx+c\) are all examples of quadratic expressions. We use the expression \(a{x}^{2}+bx+c\) so often that it has a special name. It is called a quadratic trinomial in standard form.
There is more than one way to factorise trinomials, these methods are discussed in the next videos.-
Methods to factorise quadratics
In the next 2 videos the different methods to factorise quadratics are discussed using examples. Whichever method you use to factorise quadratics make sure you master it! It is an extremely important concept that you will come back to again to be successful in some of the other topics in Mathematics.
The next video shows an alternate method involving grouping that you can use to factorise quadratics. -
Find the factors
Click on the exercise Factoring quadratics to test your knowledge on finding factors of trinomials.
-
For enrichment
When \(a\) the coeffcient of \({x}^{2}\) is not \(1\) you will have to use the factors of \(a\) and the constant \(c\) to factorise the quadratic trinomial.
There is an interesting method for factorising these types of trinomials that you can read about here.
-
-
An algebraic fraction simply means that there are variables in the numerator or the denominator of a fraction.
For example, \(\frac{2}{x-2}\) is an algebraic fraction.
-
Adding and subtracting with algebraic fractions
To add or subtract algebraic fractions you must find the lowest common denominator (LCD-also called lowest common multiple) if the denominators are different. The example in the video will take you through the method of finding an LCD for algebraic fractions.
-
More on finding the LCD
If you need more help on finding the LCD of algebraic fractions then watch the next video.
-
Practise adding and subtracting rational expressions
In the exercise you will practise all the skills you have learnt so far: Add & subtract rational expressions.
-
Multiplying and dividing with algebraic fractions
To multiply and divide algebraic fractions you will rely on all the methods you have learnt in factorisation and the rules you have used with ordinary fractions.
In the next video you will go over an example of how to multiply and divide rational algebraic expressions.
-
Practise multiplying and dividing rational expressions
In the exercise you can test your knowledge on Multiplying & dividing rational expressions.
-
