Section outline
-
-
Scientists often make measurements. These need to be stated with the units of the quantity being measured, and the accuracy of the measurements.
Measurement is the process of finding the length, size, or quantity of a substance. Since ancient times, people have used several ways to measure length. A physical quantity (like length) has to be measured with respect to some fixed quantity.
A fixed quantity with respect to which a physical quantity is measured is called a unit. A unit is used as a standard of measurement. In early times, people used different body parts like hand span, cubit, and fathom to measure length.
Foot, pace, and yard are some other units of length based on body parts. However, these units are not reliable as the length of body parts varies from person to person. Therefore, people realised the need for standard units of measurement.
Standard Units of Measurement
Standard Units of Measurements Units that have a fixed quantity and do not vary from person to person and place to place are called standard units. For example, the metric system, created by the French in 1790, is a standard set of units.
Adopting standard units of measurement does not solve the problem. People in different countries may be using a different set of standard measurement units. For the sake of uniformity, scientists all over the world have adopted a common set of units. This system is called the International System of Units or the SI units. The adoption of SI units in 1960 made it easier for scientists of different countries to communicate their results to one another.
The SI unit of length is metre. Some common standard units of length are inch, millimetre, centimetre, and kilometre.
Depending on the size of the object, we need to measure, we have to choose an appropriate unit.
For example, we use metres to measure the length of a piece of cloth, kilometres to measure the distance from one place to another, millimetres to measure the thickness of the hair, and so on. Centimetre (cm) and millimetre (mm) are used to measure shorter distances while kilometre (km) is used to measure longer distances.
One kilometre is divided into 1000 equal divisions, each called metre. One metre is divided into 100 equal divisions, each called centimetre which is again divided into equal divisions. Each division is called millimetre.

The meter is defined as the distance light travels in 1/299 792 458 of a second.
Commonly used units of length:
10 millimetres = 1 centimetre (cm)
100 centimetres = 1 metre (m)
1000 metres = 1 kilometre (km)
A unit can be converted to another. Here is an example.
Example 1: Raju and his friend Akhil live 2000 m from each other. Express the distance between their houses in kilometres (km).
Solution: We know that 1000 m = 1 km
Therefore, 2000 m = 2 km
Therefore, the distance between the two houses is 2 km.
Time - in physics time is measured in seconds (s). You can count seconds by saying at a steady rate one thousand, two thousand, three thousand. However, for accuracy when doing an experiment, you should always use a stopwatch.
Mass
If you buy a bag of sugar at the shops, you will see the mass of the sugar marked on the bag. It will be written in grams (g) or kilograms (kg). Kilo always means a thousand.
1 kg = 1 000 grams.
When you are measuring it is important to use appropriate and sensitive equipment to ensure your measurements are accurate.
If you were measuring the length of a soccer field, would it be appropriate to use a 15 cm ruler or the measuring wheel? It you were measuring the length of a stone; would you use the tape measure or the Verner calipers?
If you were measuring the time it took a classmate to run 100 m would you use a stopwatch or the clock on your classroom wall?
If you needed to measure 5 g of sugar, the more appropriate balance to use would be the electric mass balance. This is because they are very sensitive balances and will give a more precise mass. The compression balance is more useful if you need to measure the mass of objects over 1 kg.
-
-
-
Fundamental Quantities
Fundamental quantities are independent physical quantities that are not possible to be expressed in terms of any other physical quantity.
These quantities are used to derive all other physical quantities.
It is important to remember these seven fundamentals (or 'base') units of measurement:
- metre (m) - unit of length
- kilograms (kg) - unit of mass
- second (s) - unit of time
- ampere (A) - unit of electrical current
- kelvin (K) - unit of temperature
- mole (mol) - unit of the amount of substance
- luminous intensity (cd) unit of candela
SI Unit Prefixes
The SI system utilizes a standard system of prefixes to the basic units, allowing them to be more relevant and descriptive of relative magnitude. Prefixes are used to identify the original unit’s multiples or fractions. There are 20 accepted prefixes. The table below lists some the standard prefixes for the SI units of measurement.
Approximate length of time in seconds
Events
1018
Expected lifetime of the sun
1017
Age of the Earth
1015
Time since dinosaurs lived
1013
Time since the earliest human
1010
Time since Isaac Newton lived
109
Average human life span
107
A school term
105
One day
100
One second
10-2
Time for sound to cross the room
10-7
Time for an electron to travel through a TV tube
10-8
Time for light to cross a room
10-11
Time for light to pass through spectacles
10-22
Time for some events inside an atom
For very large or very small numbers, we use a short way of writing them by counting the numbers of zeros.
For example:
1 million = 1 000 000 (6 zeros) = 106
0.000 001 = 1/1 000 000 = 1 millionth = 10-6
Derived units
There are many quantities scientists measure that come from the base units. These derived units are very useful to quote as measurements, but they are not fundamental as they come from fundamental units.
For example, frequency is the number of times something happens per unit of time. This is a useful quantity, but it is a division into the time unit. The standard unit for frequency is considering the number 'per second', which is called 'hertz, Hz', but this comes from the fundamental unit 'second'.
Derived units include:
Name Unit Abbreviation Frequency hertz Hz Force newton N Energy joule J Power watt W Pressure pascal Pa Electric charge coulomb C Electric potential difference volt V Electric resistance ohm Ω Magnetic flux density tesla T
-
-
-
Physics laboratories contain apparatus used in determining measurements, calibration, analysis of variations and precision. The focus of the laboratory's research determines the required apparatus. Instruments range from simple balances and thermometers to advanced lasers and semiconductor equipment.
General Laboratory Equipment
The most basic physics laboratory equipment includes fume hoods, desks, tables, benches and gas, water, and vacuum lines. Safety equipment may include gloves, goggles, and eyewash stations.
Below are some examples of equipment you may find in a physics lab:

A resistor is an electrical component that provides electrical resistance in a circuit. It is used to reduce current flow, adjust signal levels, and to divide voltages.

A voltmeter is an instrument used for measuring electrical potential difference between two points in an electric circuit.

An ammeter is an instrument used to measure the current, either direct or alternating electric current, in a circuit. Electric currents are measured in amperes (A), hence the name.

A compass is an instrument that shows directions. It has a needle, called a compass rose, which points in North-South direction. The "N" mark on the rose points northward. Compasses often display markings for angles in degrees in addition to the rose. North corresponds to 0°, and the angles increase clockwise i.e. east is 90°, south is 180°, and west is 270°.

A magnet is a material or object that produces a magnetic field that exerts a force, called magnetic force, which pulls on other ferromagnetic materials, such as iron, and attracts or repels other magnets. It has two poles called North and South pole.

A prism is a transparent optical element with flat, polished surfaces that refract light. At least two of the flat surfaces must have an angle between them. The traditional geometrical shape is that of a triangular prism with a triangular base and rectangular sides. Prisms can be made from any material that is transparent. Typical materials include glass, plastic, and fluorite. It can be used to split light into the colours of the rainbow where each colour has different wavelengths.

A thermometer is a device that measures temperature or change in temperature for a given body. It consists of bulb which contains alcohol which expands with a change in temperature, and visible scale that converts this change into a numerical value.

Spring Balance is used to measure force using Hooke’s law. When force is applied to the spring it extends. Larger the force greater the extension will be.

The triple beam balance is a measuring instrument that measures mass very precisely. It has a reading error of +/- 0.05 gram. The name refers to the three beams including the middle beam which is the largest size, the front beam which is the medium size, and the far beam which is the smallest size. The middle beam reads in 100-gram increments, the front beam can read from 0 to 10 grams, and the far beam reads in 10-gram increments. It can measure an object's mass directly or find mass by difference for liquid.
-
-
-
All matter contains particles. The difference between the different states of matter is how the particles are arranged:
- in a solid ‐ particles are tightly packed in a regular structure
- in a liquid ‐ particles are tightly packed but free to move past each other
- in a gas ‐ particles are spread out and move randomly
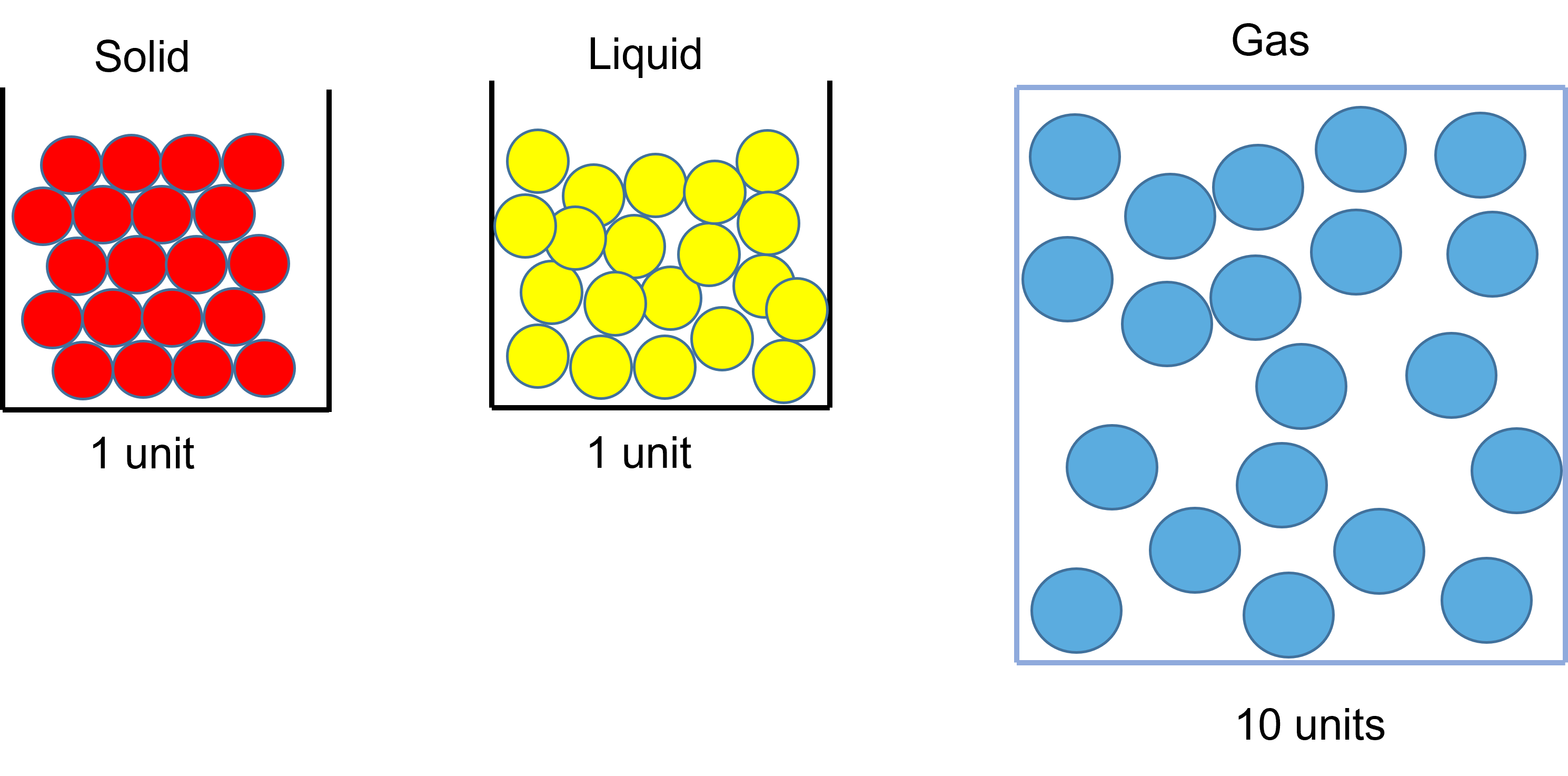
The density of an object or substance is its mass divided by its volume.
The units of density depend on the units used for mass and volume. The most commonly used units are grams per cubic centimetre (g/cm³) or kilograms per cubic metre (kg/m³).
There is little difference between the density of a liquid and its corresponding solid (eg water and ice). This is because the particles are tightly packed in both states. The same number of particles are spread further apart than in the liquid or solid states. The same mass takes up a bigger volume - this means the gas is less dense.
Density also depends on the material. A piece of iron with the same dimensions as a piece of aluminium will be heavier because the atoms are more closely packed, and because an individual iron atom is heavier than an aluminium atom.
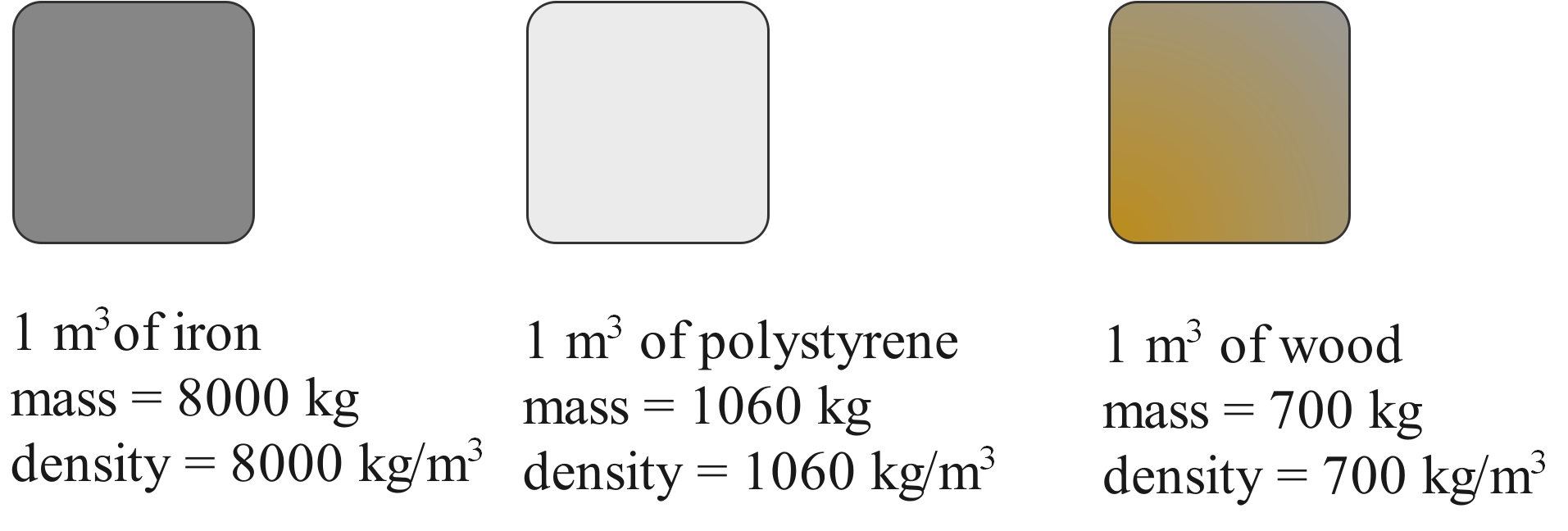
The iron cube is much heavier than the wooden cube, even though they are both the same size. This is because the iron cube has a much higher density. The cube of polystyrene is the same size but is lighter than both because it has an even lower density.
Scientists can measure how tightly packed the particles are by measuring the mass of a certain volume of the material, for example, one cubic centimetre.
Material Density (g/cm³) Iron 7.8 Ice 0.98 Water 1 Air 0.00129
The density of a substance depends both on the mass of the particles, and how closely spaced they are. This means that density changes when substances change state, and when they are heated or cooled.
Calculating density
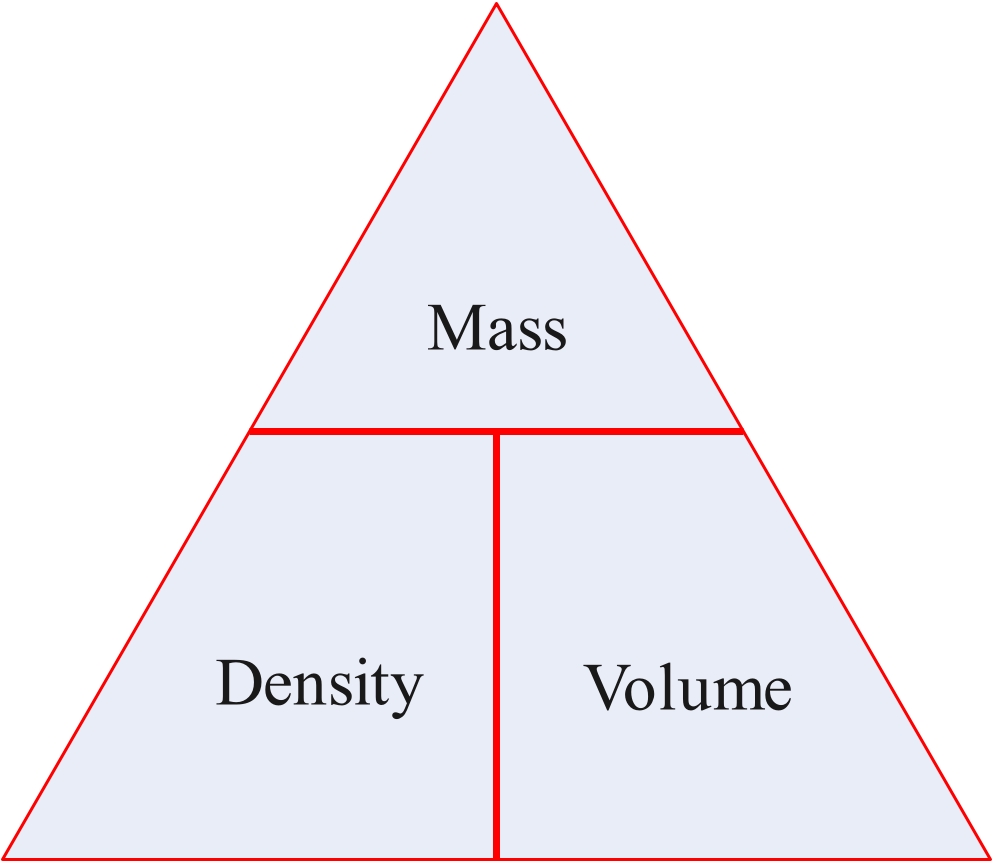
Density = mass/voume
mass = density x volume
volume = mass/density
This is when:
- density (ρ) is measured in kilograms per cubic metre (kg/m3 )
- mass (m) is measured in kilograms (kg)
- volume (V) is measured in cubic metres (m3)
Example
What is the density of a material if 0.45 cubic metres (m3 ) of it has a mass of 0.2 kg?
d = m/v
d= 0.2/0.45
d = 0.44 kg/m3
Question:
What is the density of a material if 4 cubic metres (m3 ) of it has a mass of 2,200 kg?
d = m/v
d = 2200/4
d = 550 kg/m3
The standard unit for mass is kilograms (kg) and for volume is cubic metres (m3). However, in many laboratory situations it is common to measure the mass in grams (g) and volume in cubic centimetres (cm3).
Calculating density using grams and cubic centimetres would give a density unit of grams per cubic centimetre (g/cm³).
1 g/cm3 is equal to 1,000 kg/m3
- To convert from kg/m3 to g/cm3, divide by 1,000.
- To convert from g/cm3 to kg/m3, multiply by 1,000.
Aluminium has a density of 2.7 g/cm3, or 2,700 kg/m3. Lead has a density 11.6 g/cm3, or 11,600 kg/m3.
Example:
Iron has a density of 7.9 g/cm3 what is this in kg/m3 ?
7.9 multiplied by 1,000 gives 7,900 kg/m3.
Question:
What is the density of an object in kg/m3 if it is 6.531 g/cm3 ?
Answer:
6.531 x 1,000 would give 6,531 kg/m3.
Relative density
If placed in water, the iron cube will sink, but the polystyrene and wood cubes will float. This is because the iron cube is more dense than the water and the wood and polystyrene cubes are less dense than water.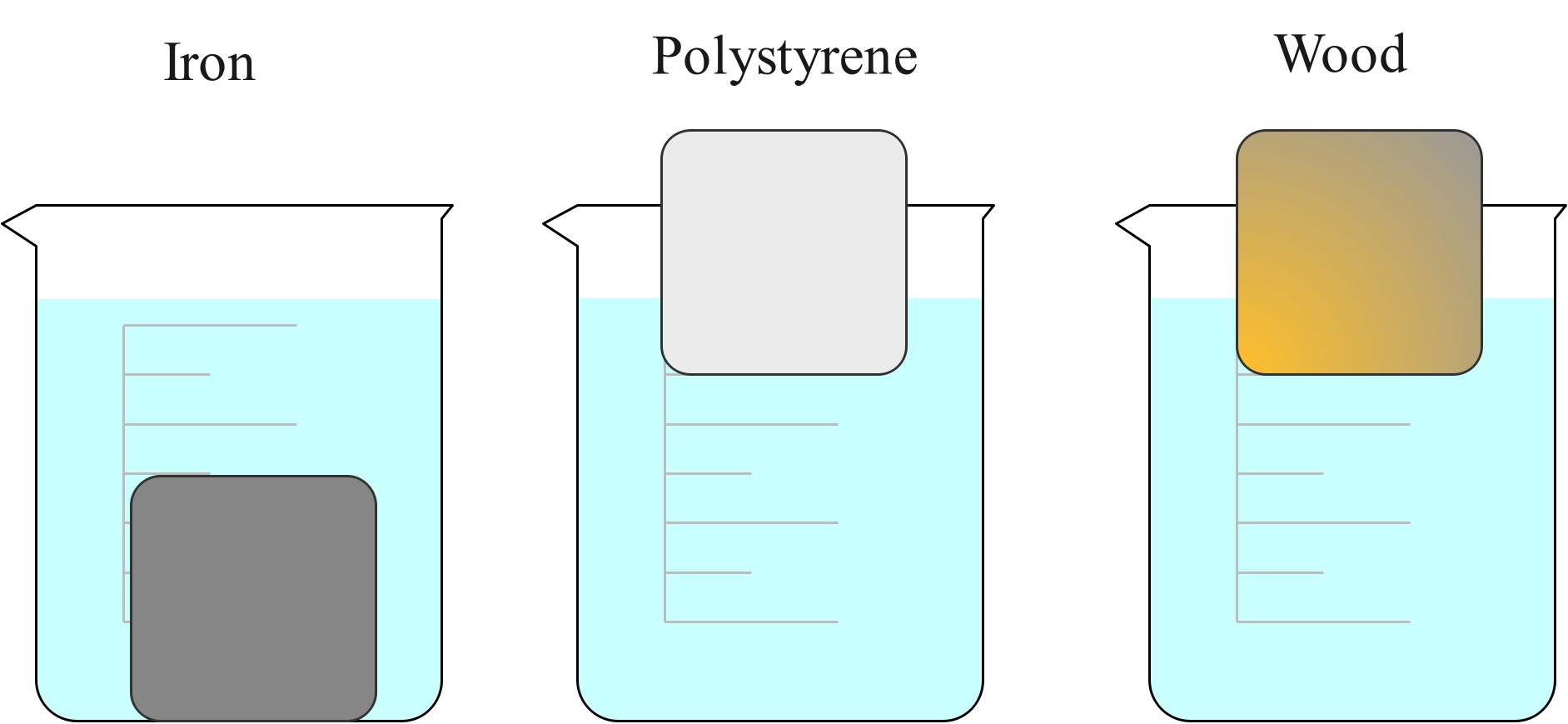
Relative density is the ratio of the density of a substance to the density of water. It is also known as specific gravity. It is a unitless value. If it is less than 1, the substance is less dense than water and would float. If it is greater than 1, the substance is denser than water. If it is exactly 1, the densities are equal. It is usually measured at room temperature and standard atmosphere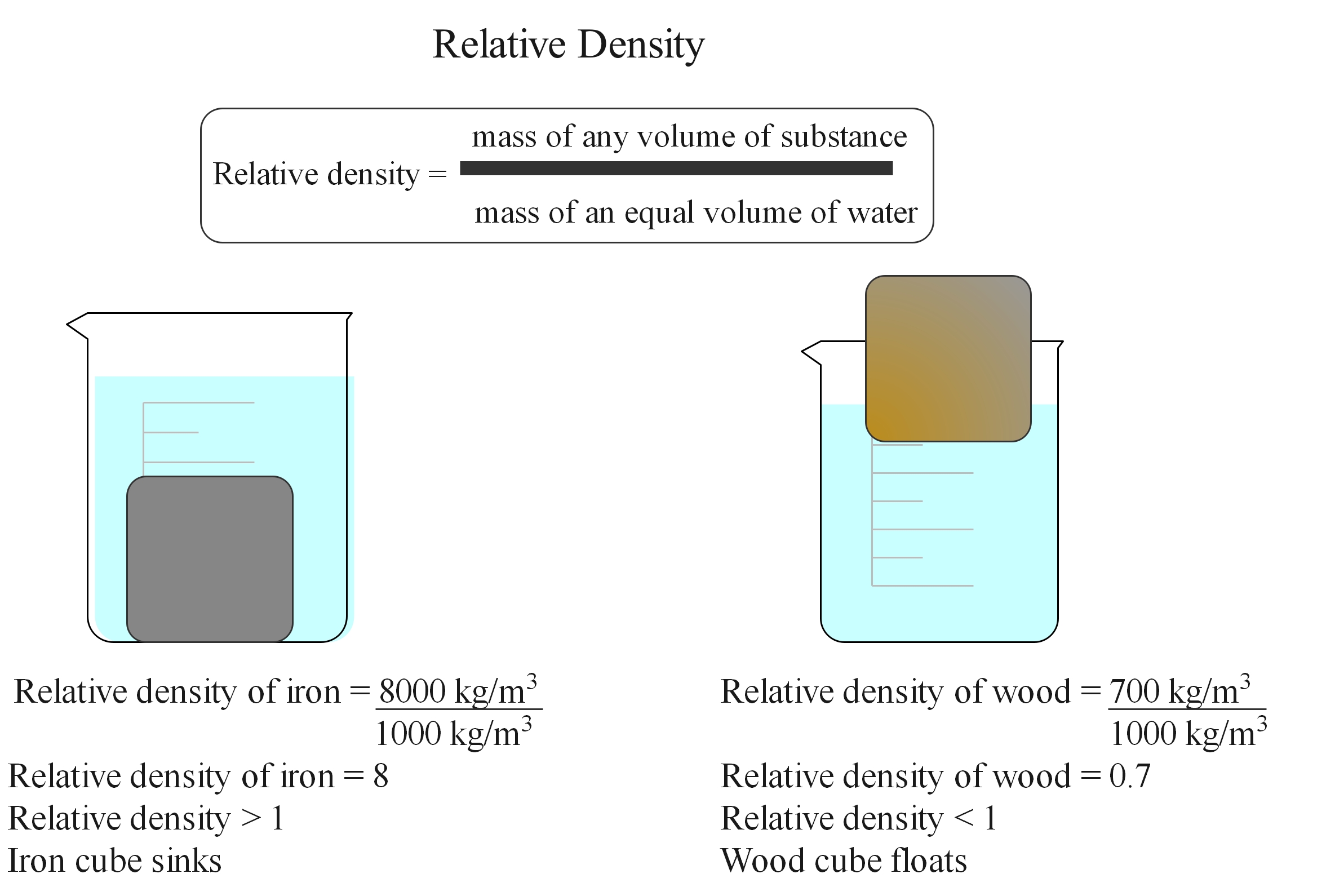
-
-
-
Measuring the density of different objects
There are different ways to investigate density. In this required practical activity, it is important to:
- record the mass accurately
- measure and observe the mass and the volume of the different objects
- use appropriate apparatus and methods to measure volume and mass and use that to investigate density
Aim of the experiment
To measure the density of various materials.
Method
Method 1: Stone or other irregular shaped object
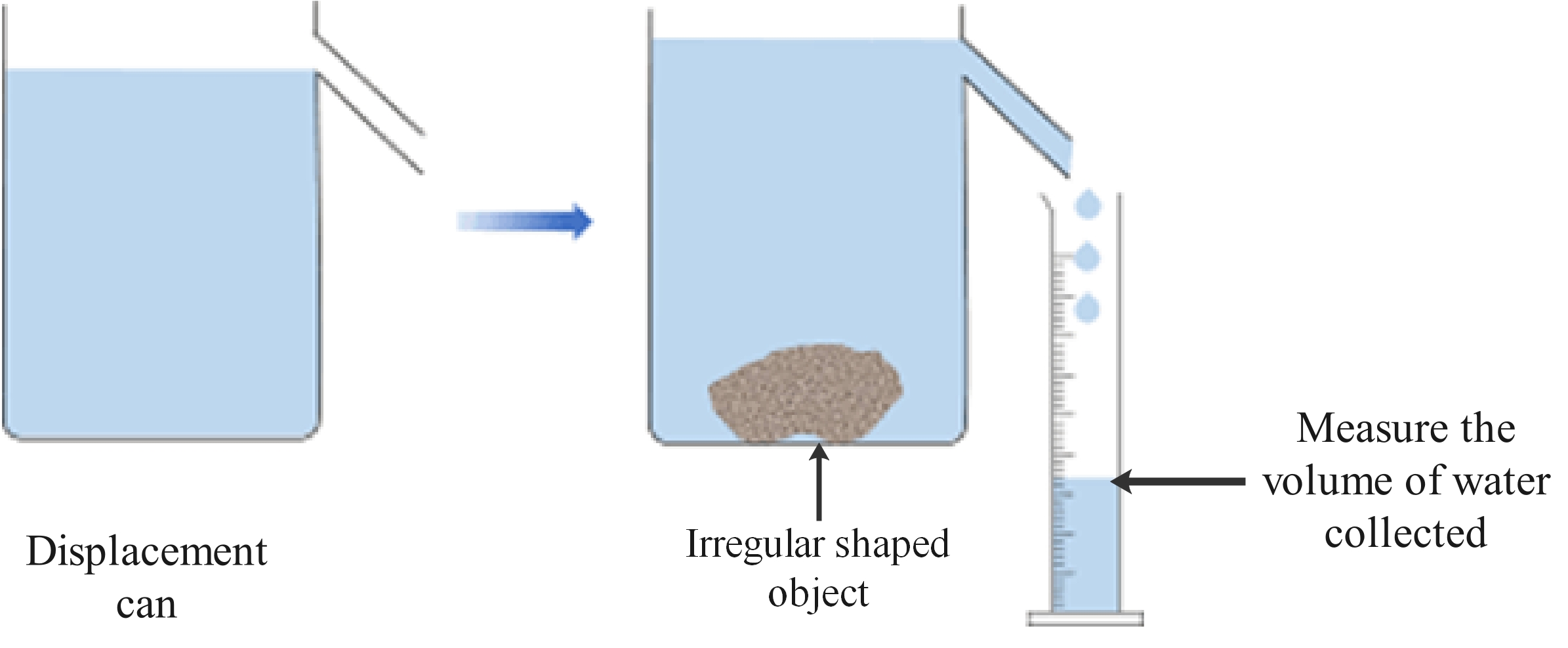
- Place the stone on the mass balance and measure its mass.
- Fill the displacement can until the water is level with the bottom of the pipe.
- Place a measuring cylinder under the pipe ready to collect the displaced water.
- Carefully drop the stone into the can and wait until no more water runs into the cylinder.
- Measure the volume of the displaced water.
- Use the measurements to calculate the density of the stone.
Method 2: Water (or any liquid)
- Place the measuring cylinder on the mass balance and measure its mass.
- Pour 50 cm3 of water into the measuring cylinder and measure its new mass.
- Subtract the mass in step 1 from the mass in step 2. This is the mass of 50 cm3 of water.
- Use the measurements to calculate the density of the water.
Results
Some example results could be:
Object Mass (g) Volume (cm³) Density (g/cm³) Density (kg/m³) Steel cube 468 60 Steel sphere 33 4.19 Stone 356 68 Water 50 50 Analysis
Using those results, the densities can be calculated using:
Density = mass ÷ volume
Density = mass ÷ volume = 33 ÷ 4.19 = 7.9 g/cm3 (= 7,900 kg/m3 )
For a stone of mass 356 g, the volume of water displaced into the measuring cylinder is 68 cm3
Density = mass ÷ volume = 356 ÷ 68 = 5.2 g/cm3 (= 5,200 kg/m3 )
Mass of 50 cm3 of water is found to be 50 g.
Density = mass ÷ volume = 50 ÷ 50 = 1 g/cm3 (= 1,000 kg/m3 )
-
