Sectieoverzicht
-
-
It makes calculations easier to try to measure the perpendicular distance between the line of action of the force and the pivot. For example, if you apply a force to a spanner it rotates. The pivot is at the bolt.
If you want to undo a very tight nut, would you choose a spanner with a short handle or a long handle?
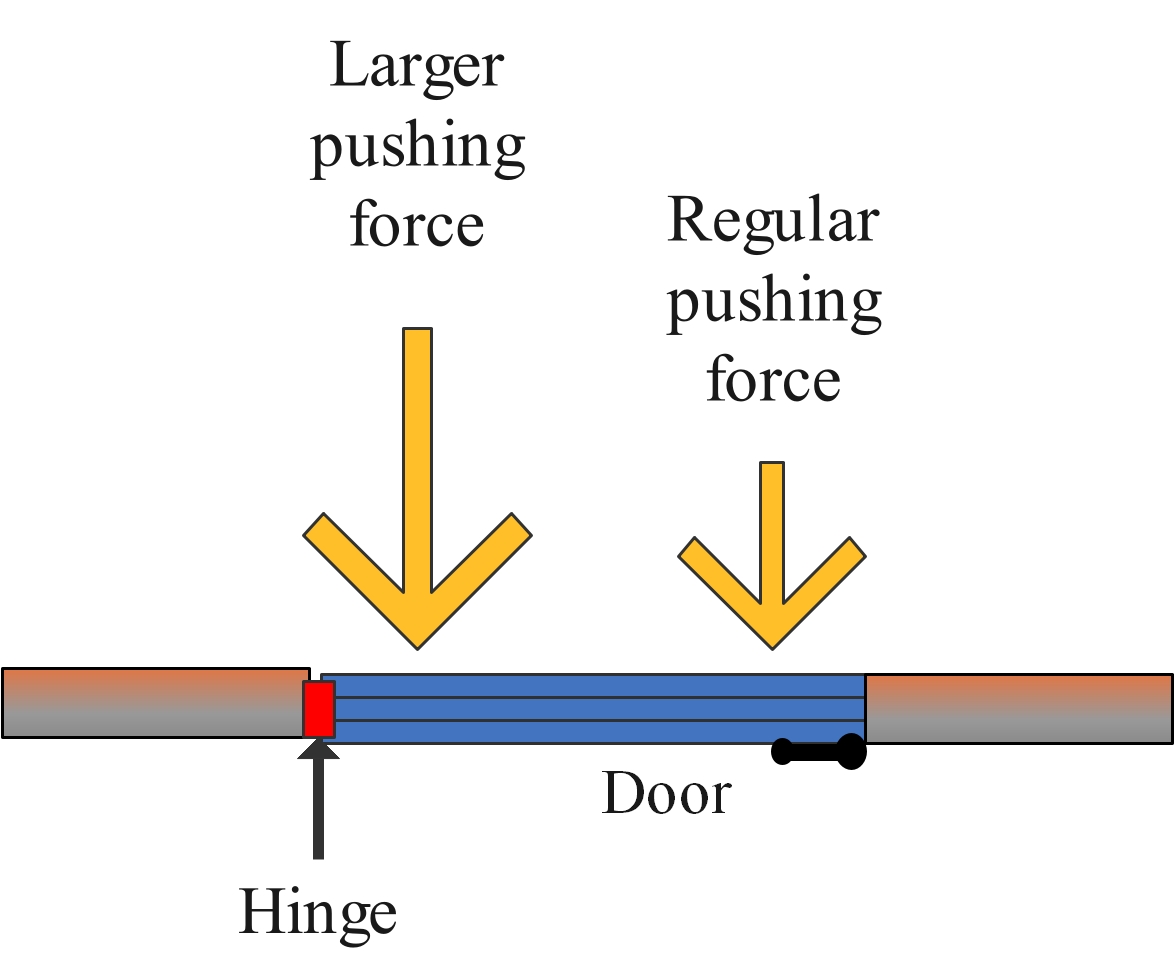
Why is a door handle on a door placed far away from the hinges where the door pivots?
Activity 1
What you will need:
a rod
different hanging weights
What you will do:
1. Hold a rod horizontally and hang a weight on the rod near your hand.
2. Move the weight to different distances from your hand keeping the rod horizontal.
What happens?
3. Try it with heavier weights.
You can feel the turning effect on your hand. The turning effect depends on the size of the force (the weight) and the distance from your hand.
The turning effect of the force is called a moment or a torque.
This is calculated by:
The distance used is always the shortest (perpendicular) distance. Moments are measured in newton-metres, written Nm.
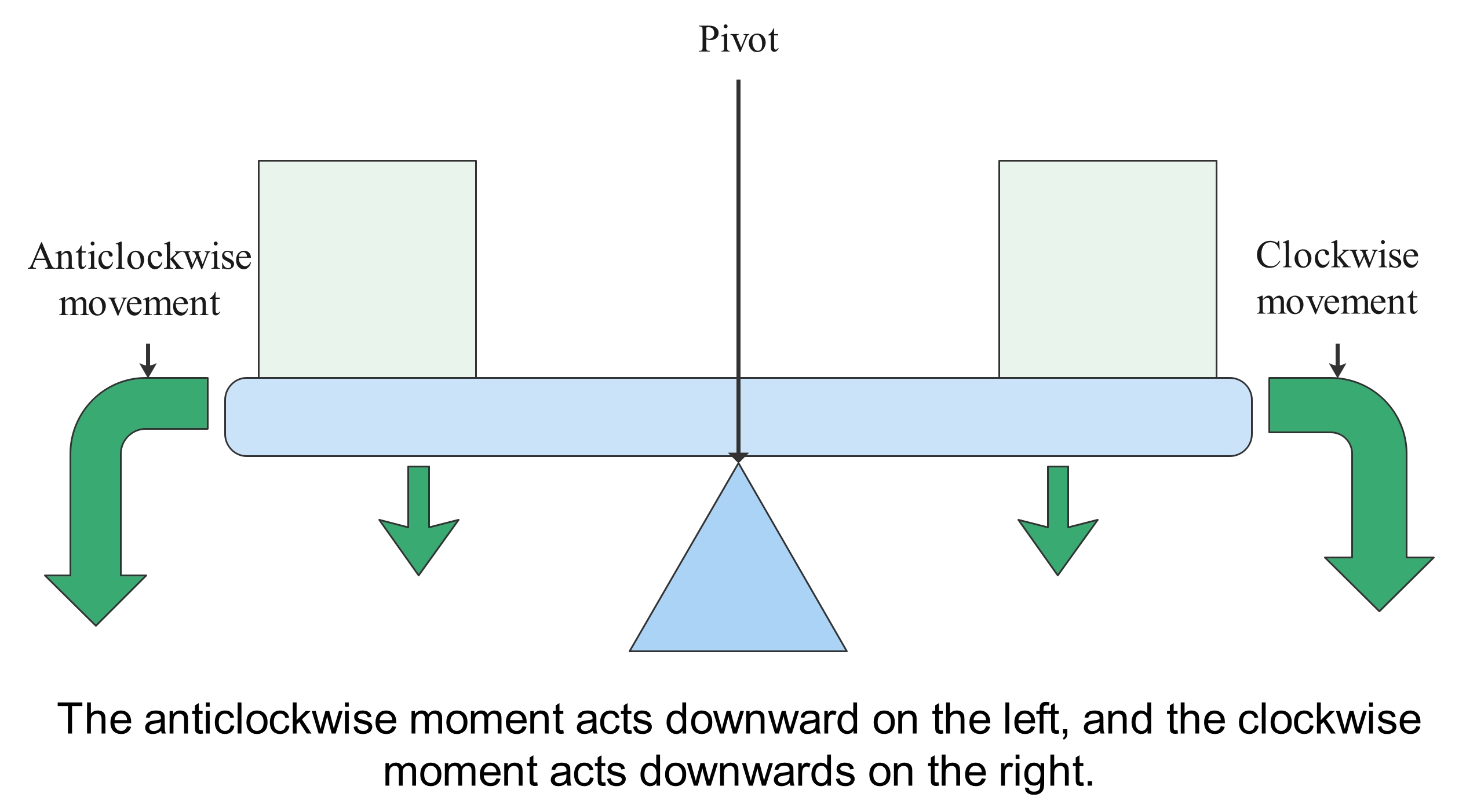
Moments act about a pivot in a clockwise or anticlockwise direction.
Example:
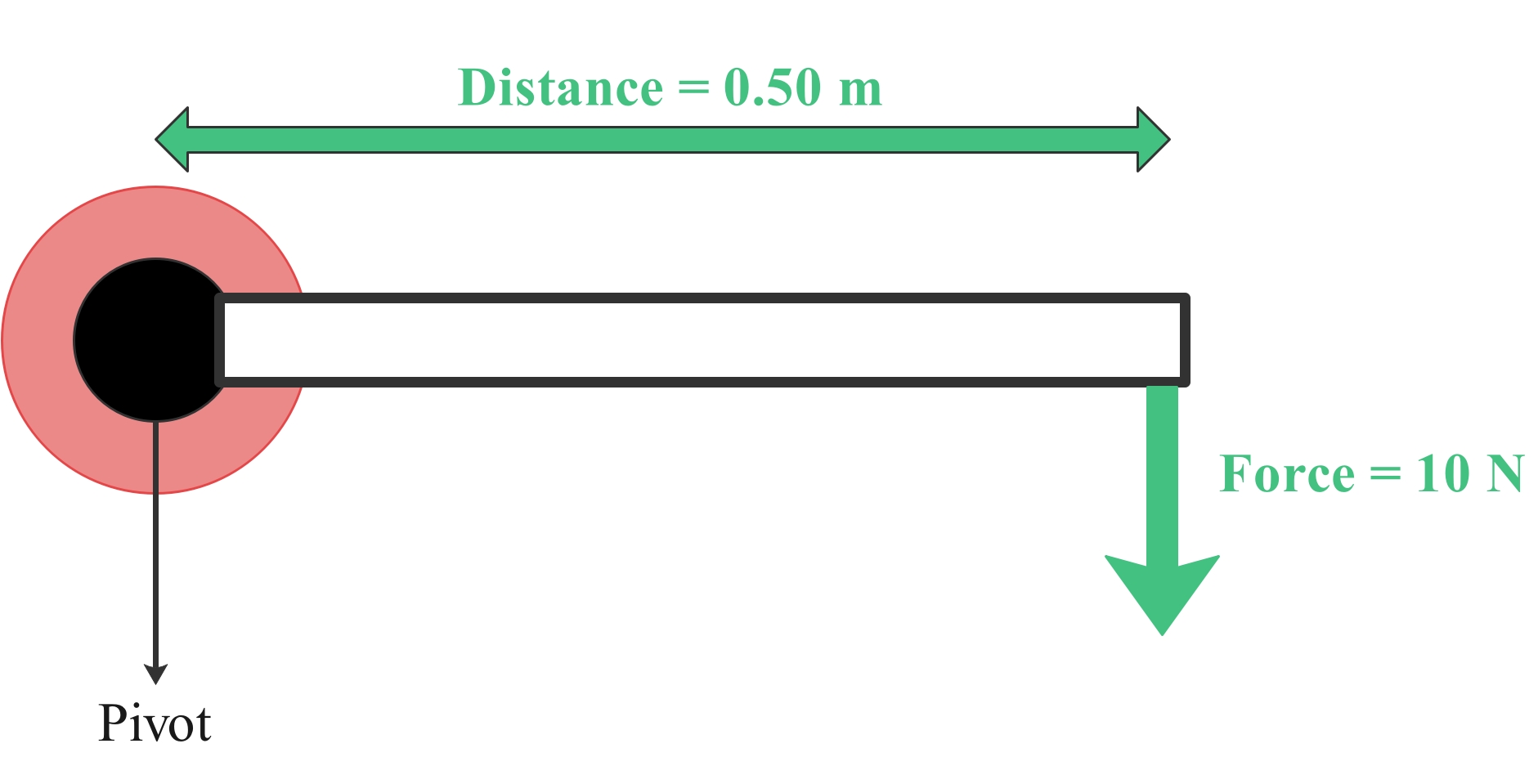
Perpendicular distance from pivot to force d = 0.50 m.
Force F = 10 N
Moment = Fd
Moment = 10 N x 0.50 m
Moment = 5 Nm. This is a clockwise moment.
The force will rotate the object in a clockwise direction about the pivot.
It is important to remember that the distance d is the perpendicular distance from the pivot to the line of action of the force (see diagram).
Example:
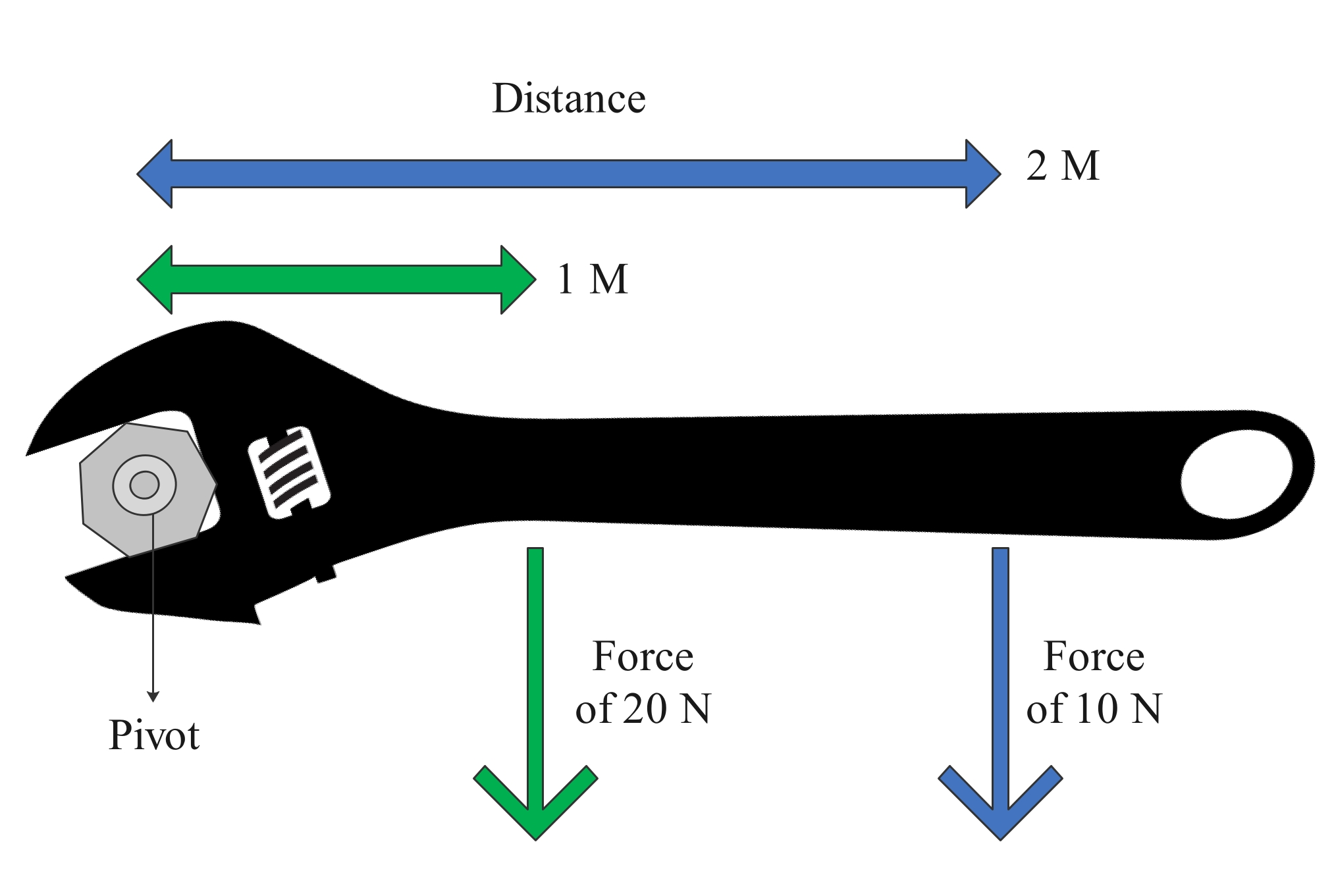
What is the turning effect of the force in the diagram, about the nut at point P.
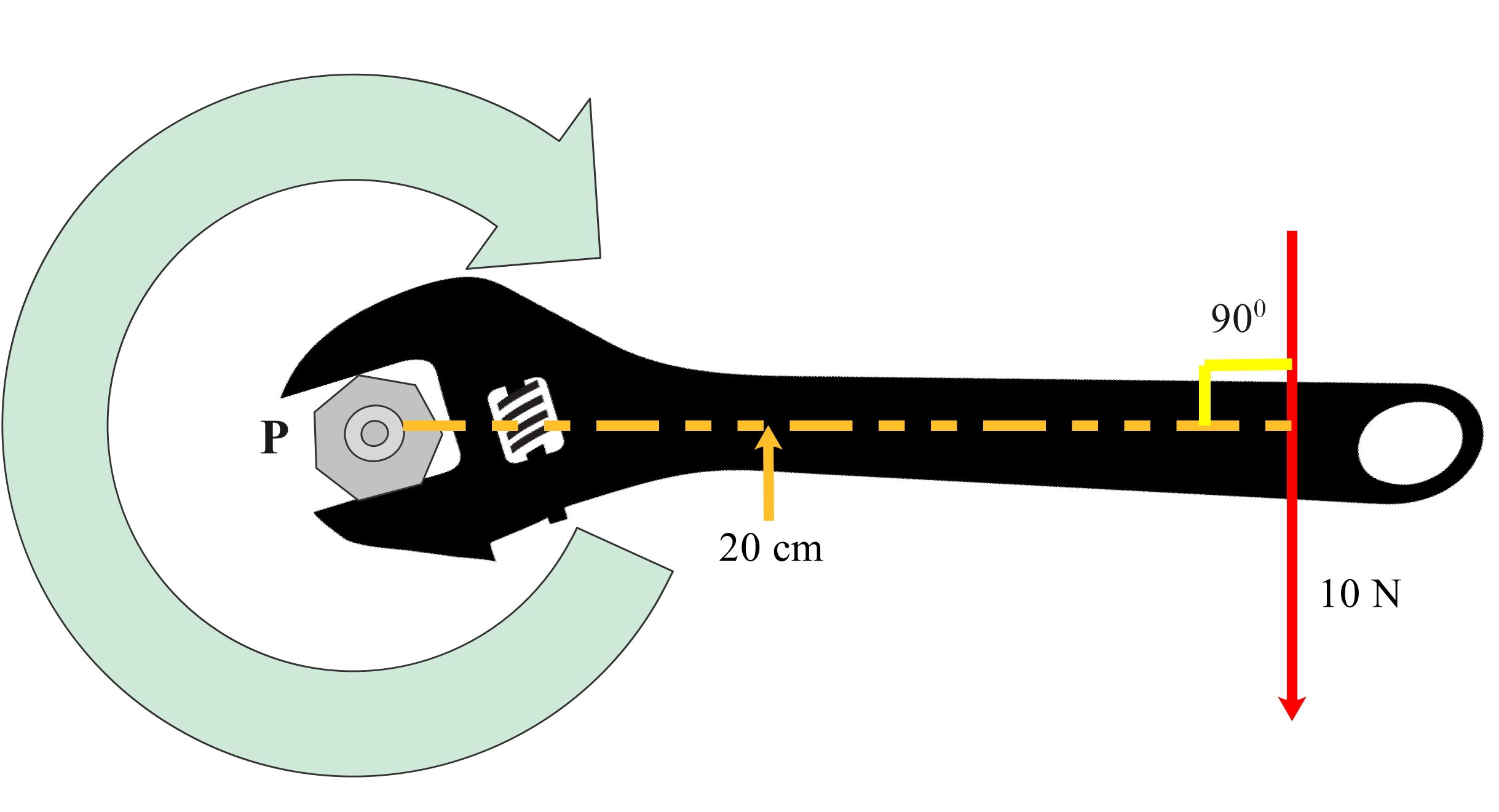
Perpendicular distance from the force to P = 20 cm = 0.20 m
Moment of force = force x perpendicular force
= 10 N x 0.20 m
= 2 Nm turning clockwise
Spanners and levers both use moments.
Spanners are used to turn nuts and bolts. If you need to undo a nut that is very tight, you can:
use a short spanner and apply a large force
or
use a long spanner and apply a small force
Using the longer spanner increases the distance from the pivot. This reduces the amount of force needed to undo the nut from the bolt.
Removing the lid from a can of paint requires a large lifting force on the lid. A screwdriver acts as a lever. The pivot is the edge of the can, and this is very close to where the strong push is needed to lift the lid to open the can.
A screwdriver with a long handle means that you can push down on the handle of the screwdriver with a small force and still open the can.
-
-
-
-
When a see saw is balanced and is not moving it is in equilibrium.
This is called the principle of moments.
In equilibrium the total anticlockwise movement = total clockwise moment
Will this seesaw be in equilibrium?
In short no! The elephant is much heavier than the child.
For the seesaw to be in equilibrium, the elephant will need to be closer to the pivot.
Fuseschool. (2019). Moments (Standard YouTube licence)
Activity:
1. Click on the link below:
https://phet.colorado.edu/sims/html/balancing-act/latest/balancing-act_en.html
2. On the right-hand menu click on the ruler, mass labels, forces on objects and level
3. Place the bricks of any mass on each side of the plank
4. Remove the supports using the slider in the bottom centre
What happens to the plank?
5. Move the bricks on each side of the plank to make the plank balance
6. Change the mass of the bricks and again move them to make the plank balance
The plank will balance even when the mass of each side is different, by placing then at different distances from the pivot.
Example:
A seesaw needs to balance. One side, 3 m from the pivot, is a box which has a weight of 5 N, and on the other is a box which has a weight of 3 N. Calculate the distance needed between the mass which has a weight of 3 N box and the pivot.
Remember: anti-clockwise moment = clockwise moment
1. Calculate the clockwise moment using the following equation:
M = F x d
M =?
F = 5 N
d = 3 m
Substitute in the values you know:
M = 5 x 3
M = 15 Nm. The clockwise moment is 15 Nm
2. The seesaw needs to be balanced:Remember - total anti-clockwise moment = total clockwise moment.We have already calculated that the clockwise moment is 15 Nm.Use the equation:M = F x dSubstitute in the values you already know:M = 15 Nm
F = 3 N
d =?
Now divide both sides by 3:
This cancels to give 5 = dSo, the distance between the box weighing 3 N and the pivot is 5 m.
Example
If the ruler in the diagram below is balanced, what is the weight W?
Remember in equilibrium the total anticlockwise moment = total clockwise moment
W x 25 = (4 x 15) + (1 x 40)
W x 25 = 60 + 40
W x 25 = 100
W = 4 N -
Investigation: Principle moments
Purpose: To plan and carry out experiments to verify the Principle of Moments using a suspended metre rule and attached weights.
The Principle of Moments states that when a body is balanced, the total clockwise moment about a point equals the total anticlockwise moment about the same point.
Remember: Moment =force F x perpendicular distance from the pivot d.
Moment = Fd
What you will need:
uniform metre rule
retort stand
boss and clamp
two 100 g mass hangers
100g slotted masses,
a g-clamp,
three lengths of string.
What you will do:
1. Set up the retort stand and clamp it to your desk. Suspend the metre rule at the 50 cm mark so that it is balanced horizontally. The ruler is said to be in equilibrium. The 50 cm mark is the pivot.
Remember that 1 newton = 100 g
2. Suspend a 100g mass, m1, from one side of the ruler a distance 40 cm, d1, from the pivot. Read the distance d1 in cm, from m1 to the pivot. Create a table like the one below and record this distance in the table. Record the value of mass m1 in kg.
Anticlockwise
Weight W (N)
Distance d (cm)
Moment W x d
2
20
2
15
Clockwise
Weight W (N)
Distance d (cm)
Moment W x d
1
40
40
1
3. Suspend a 200g mass, m2, from the other side of the pivot. Carefully move this mass backwards and forwards until the ruler is once more balanced horizontally. Read the distance d2 in cm from the mass m2 to the pivot. Record d2 in cm, in your table, along with the mass m2 in kg.
4. Repeat with other weights at different distances and record the weight and distances in your tables.
Conclusion:
Each time the ruler balances horizontally we can see from our results that, the anticlockwise moment about the pivot = the clockwise moment about the pivot.
This verifies the Principle of Moments.
BBC Bitesize Secondary Level. (2020). What is the principle of moments? (Standard YouTube licence) -
-
-
-
The centre of gravity is the point through which the whole weight of object seems to act.
Centre of gravity is sometimes called the centre of mass.
If you were carrying a ladder, which part of the ladder would you rest on your shoulder to carry it most comfortably?
Depending on the object's shape, its centre of gravity can be inside or outside it.
Regular shapes
A metre rule is a uniform and regular shape, therefore its centre of gravity, G, is at its centre i.e. at the 50 cm mark.
Do you notice that for a regular shaped object, the centre of gravity is also the middle of the object?
Activity
What you will need:
A mass piece
string
a retort stand
a pin
a piece of card
a pencil and a ruler
What you will do:
1. Try and balance the ruler on the pencil.
Where is its centre of gravity?
2. Tie the weight to a small piece of string to form a plumbline. Let it hang from your hand.
Why does it always hang vertically?
Finding the centre of gravity of a piece of card using a plumbline.
3. Pin the card to the retort stand but allow it to hang freely.
4. hand the plumbline from the same pin.
Mark the position of the plumbline by two crosses on the card. Join the crosses with the ruler.
Just as the plumbline hangs with its centre of gravity vertically below the pivot, so will the card. This means that the centre of gravity of the card is somewhere on the line you have marked.
5. To find where the centre of gravity is on the line, re-hang the card with the pin through another hole, and again mark the vertical line.
The only point that is on both lines is where they cross, so this point is the centre of gravity.
6. Repeat the same with an L-shaped piece of card.
TutorVista. (2010). Centre of gravity: Definition, examples and experiment (Standard YouTube licence) -
-
-
-
Stability
Stability is a measure of how likely it is for an object to topple over when pushed or moved.
Stable objects are very difficult to topple over, while unstable objects topple over very easily.
An object will topple over if its centre of gravity is ‘outside’ the base, or edge, on which it balances.
This plumbline is in stable equilibrium because if it is pushed to one side it will return to its original position. It does this because when you push it to one side its centre of gravity rises and tries to pull it back to its lowest position.
If you carefully balance a ruler on your finger, it is in unstable equilibrium, because if it moves slightly, its centre of gravity falls and keeps falling.
The football on a perfectly level surface is in neutral equilibrium, because if it is moved, its centre of gravity does not rise or fall.
Activity
What you will need:Two boxes of matches
a piece of woodWhat you will do:
1. Place the matchbox upright on the piece of wood
2. Slowly tilt the wood until the box topples over. How high did you tilt the wood?
3. Put the box on the wood so it has a longer base. Tilt the wood until the box falls. Did you lift it higher or lower than the first time?
4. Raise the centre of gravity by sliding open the second box of matches. Tilt the wood. Is the box more or less stable?To make the box more stable, should it have:
- A high or low centre of gravity?
- A narrow or wide base?
- Han Wern Kuang. (2018). Moments (Standard youTube licence)
For an object to be stable it must have:- a wide base
- a low centre of gravity
Objects with a wide base, and a low centre of gravity, are more stable than those with a narrow base and a high centre of gravity.
The purple car has a wider wheelbase and lower centre of gravity than the yellow car. It is more stable.
The wheel acts as the pivot for the car. The weight has a turning effect or moment, which causes the car to topple over or fall back.
A double decker bus is stable as it has a:
- low centre of gravity because of its low, heavy engine and heavy bottom deck.
- wide wheelbase.
A traffic cone is stable as it has a:
- low centre of gravity G because of its heavy base.
- wide base.
GCSE Physics Ninja. (2016). Centre of mass and stability. (Standard YouTube licence)
-
-
