Section outline

  • Outcomes

    Collapse all Expand all


    In this course you will about:

    1. The decimal number system.
    2. Converting fractions to decimals.
    3. Calculations with decimals.
    4. Percentages.

  • Introduction to base-10 number system

    The numbers we use everyday are based on the base-10 number system, which is also known as the decimal number system. Numbers are represented using powers of 10 as place values in the decimal system.

    For example, the number \(1 525.643\) can be written as shown in the image. The numbers after the decimal point represent fractions less than 1 unit. [Edit: image below - thousands and hundreds to be lower case]

    Decimal example

    For a detailed explanation on how the decimal number system works watch the next video and then try the exercise that follows.

    • Students must
      Mark as done

      Exercise: Practise writing numbers in decimal form

      Try the next exercise to test your knowledge on writing numbers in decimal form. If you need help completing the exercise then click on the hints provided.

      Decimals in written form

  • Convert fractions to decimals

    Usually the quickest way to convert a fraction to a decimal is to use a calculator. But, you can also convert fractions to decimals by hand using long division or, if the denominator can be changed to a power of 10, then you can use the method shown in the infographic.  
    Infographic showing how to convert a fraction with a denominator that is a factor of 10, to a decimal.

    Watch the video for more examples on converting from fractions to decimals when the denominator cannot be changed to a power of 10.

  • Operations with decimals

    Just as you can add, subtract, multiply and divide whole numbers you can also perform all of these operations with decimal numbers.

    We use decimals all the time. For example, when we need to give or receive change in coins from a note, we are then adding or subtracting decimals without even realising it.

    Picture of adding dollars

    • Students must
      Mark as done

      Add and subtract decimals

      We add and subtract decimals using the same method we do for whole numbers. Line up the numbers carefully according to place value. 

      Example

      \(25.6+15.465=41.065\)

      Adding decimals using place values

      The next video will take you through the steps for adding and subtracting decimals.
        
    • Students must
      Mark as done

      Multiply and divide decimals

      We multiply and divide decimals using different methods. In the video that follows you will go through an example of each method.

      Multiply decimals

      To multiply decimals we must get rid of the decimal point by multiplying each decimal by a power of 10, and then we must divide the answer by the same power of 10.

      Divide decimals

      To divide decimals; first write the division of decimals as a fraction and then multiply the numerator and the denominator by the same power of 10 – choose a power that will make the denominator a whole number.

      In the next video you will see examples of multiplying and dividing decimals.

    • Students must
      Mark as done

      Exercise: Practise working with decimals

      Try these exercises to check your ability to add, subtract, multiply and divide decimal numbers.

      Add decimals

      Subtract decimals

      Multiply decimals

      Divide decimals

  • Percentages

    A percentage represents a fraction of 100 and is easy to identify since it is written with a percent symbol (%). Just like fractions and decimals, percentages show parts of a whole.

    Percentages can be used to quickly convey information. For example, the pie chart shows that China is the most populated country with 18.47% of the world's population.


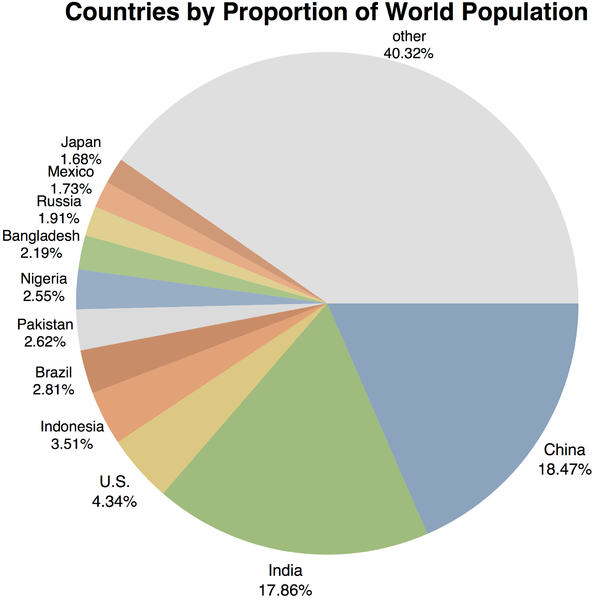
    World population percentages  


    Before you continue with changes in percentages try the next exercise to make sure you can calculate the percentage of a number.




    • Students must
      Mark as done

      Percentage changes

      Prices of things constantly change, and one of the most common ways to describe the increase or decrease in prices is by using percentages. In fact it is often easier to get a point across about changes in numbers of anything, by using percentages.


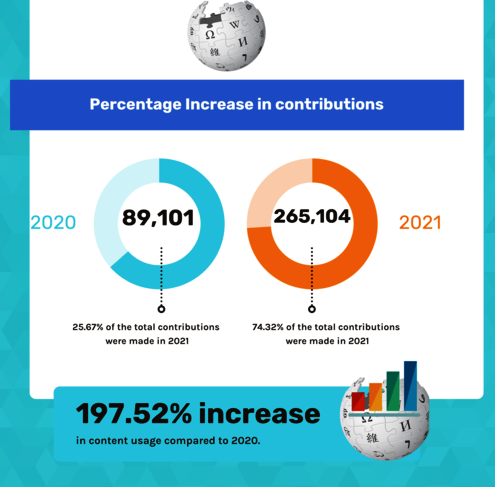
      Percentage change in Wikimedia usage 2010 to 2021

      According to the infographic there was a 197.53% increase in usage of Wikimedia content from 2021 to 2022. But, how do we calculate percentage increase or decrease? We will go over that next. [Edit: please check dates - graphic has a mix of 2020 and 2021 and text refers to 2021 and  2022]

      Percentage increase and decrease

      We use the formula: \(\frac{New  value - original  value}{Original  value}\times 100%\) to calculate a percentage change. [Edit: the spaces between words in the formula don't show up - can this be fixed?]

      Note: A negative value in the numerator indicates percentage decrease.

      • If the new value is greater than the old value, we have a percentage increase. [Edit: old value or original value - the formula uses different terms - please check and make consistent; or explain]
      • If the new value is less than the old value, we have a percentage decrease.

      Example

      An outfit originally cost $16.25, it goes on sale for $13. What was the percentage change in price?

      Original value = $16.25

      New value = $13

      \(\frac{3.25}{16.25}\times 100%=20%\)

      The outfit costs 20% less.

      You can calculate percentage increases and decreases by using multipliers. This concept is discussed in the next video. Make sure to try the exercise that follows to test your knowledge.


    • Activity: Calculate changes in percentage Interactive Content
      Students must
      Mark as done
    • Attribution & licence Page
      Students must
      Mark as done