Section outline
-
In this course you will learn about:- The terms perimeter and area.
- Finding the perimeter of any polygon.
- Finding the perimeter and area of a trapezium, parallelogram, rectangle and square.
- Finding the area of a triangle.
- Finding the perimeter and area of a circle.
-
Before we get started, it is important that we all know what the words perimeter and area mean. Do you know what the perimeter of a shape is? Do you know what the area of a shape is?
-
What is perimeter?
The perimeter is the distance around the outside of a 2D shape. We don't talk about perimeters when dealing with 3D objects.

Watch this video on perimeter to learn more and then do the activity
Try the next activity to test your knowledge. -
What is area?
The area is the region or space inside the perimeter of a 2D shape. In the image below the area of the shape is shown in yellow.

Area is always measured in square units. These can be measures like square meters (m2) or square inches (in2).
Learn more about what area is and how to measure it by watching these three videos.
-
-
-
Finding the perimeter of polygons
An irregular polygon is a closed 2D shape made up of straight sides. To find the perimeter of any polygon (including a triangle), you need to add together the lengths of each segment making up the border of the shape. In the example below, the perimeter would be
\( 2.5+3+3+4+1.5=14 \).
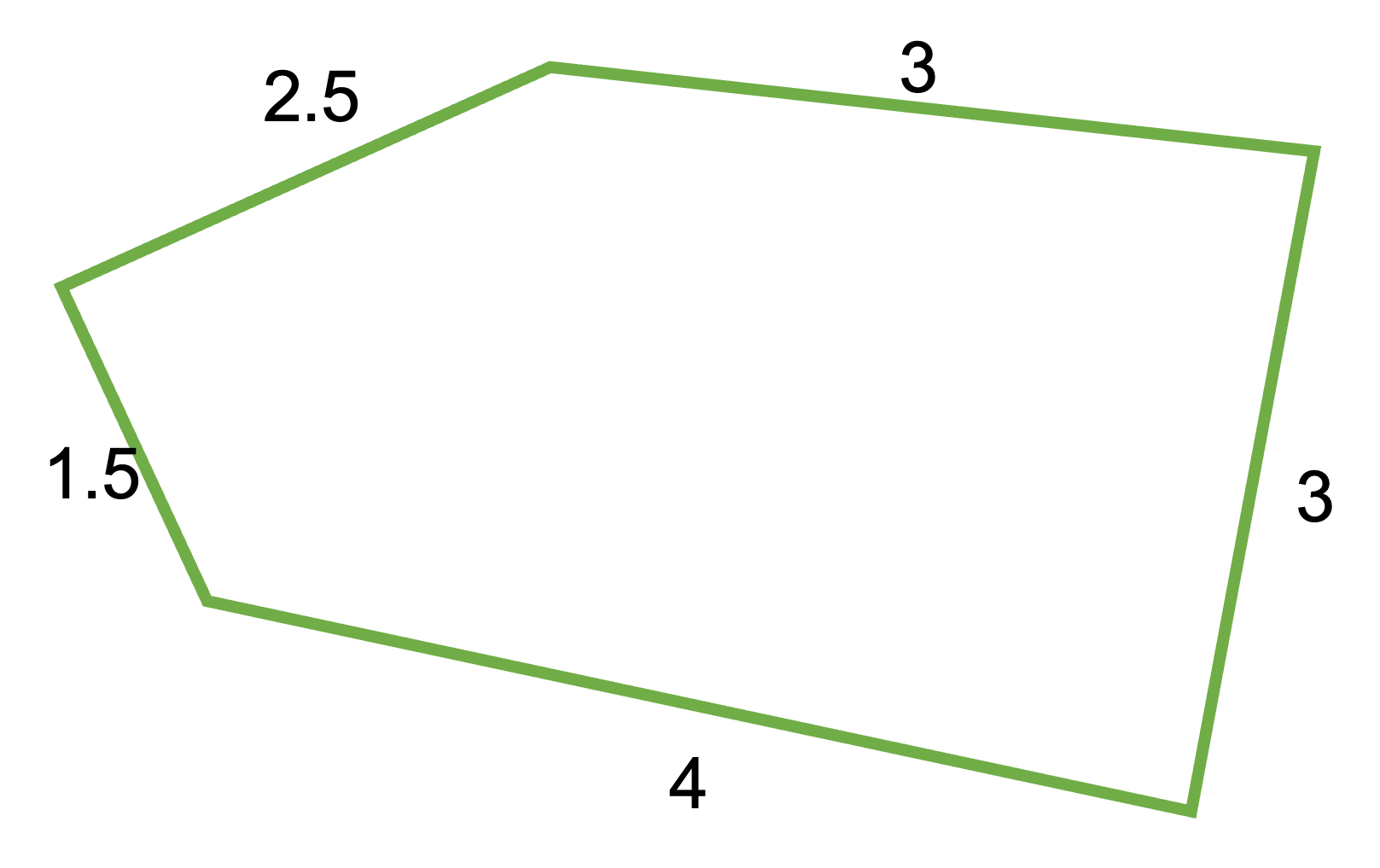
-
Exercise: Find the perimeter of polygons
Find the perimeter of the following polygons. If you like, you can draw them on a piece of paper first.
Polygon 1
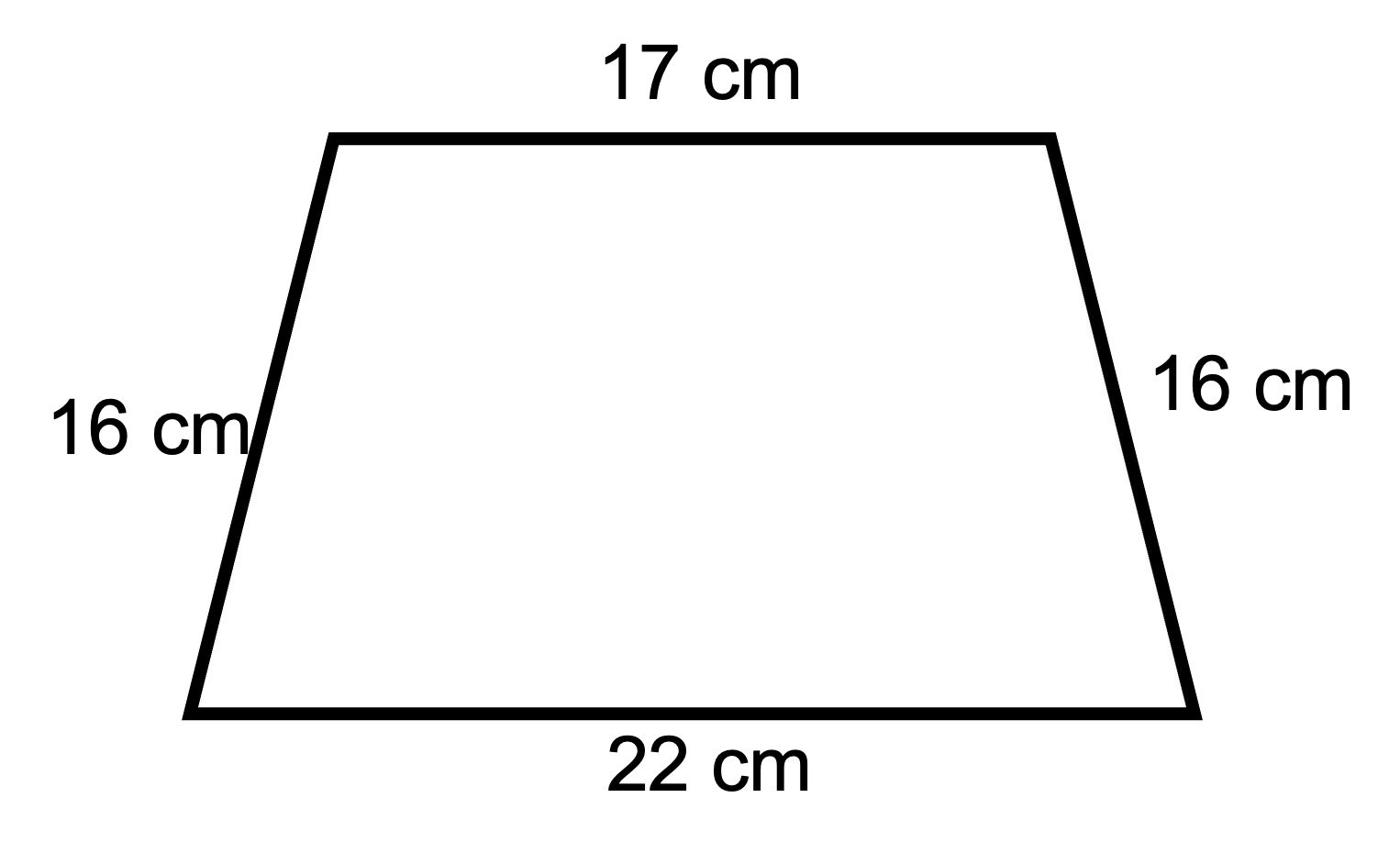
The lengths of all four sides have been given to you.
Polygon 2
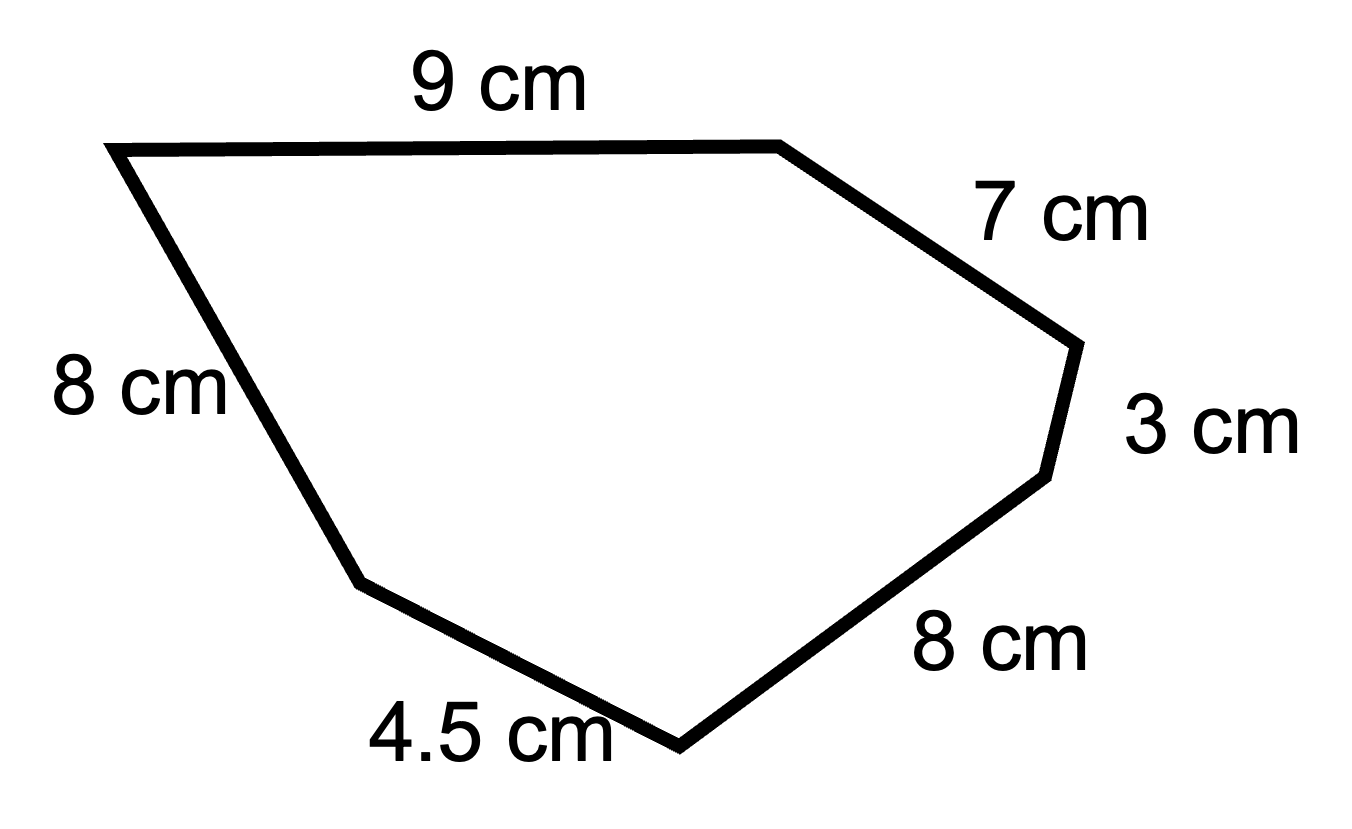
Even though it is a strange looking shape, once again, the lengths of all the sides have been given to you.
Polygon 3
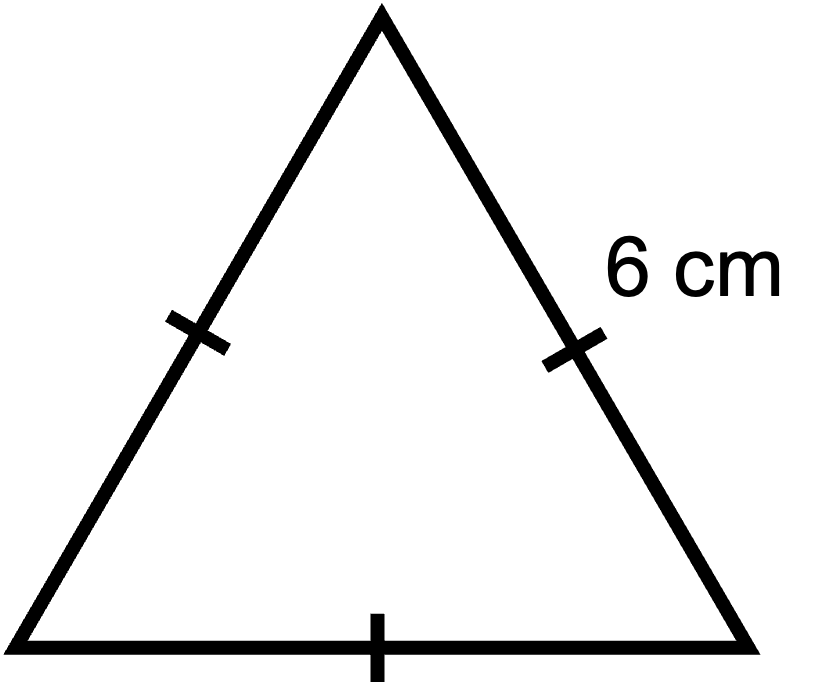
Be a bit careful with this one. Remember the markings on each side tell you that they are equal in length. Do you know the lengths of all the sides?
Polygon 4
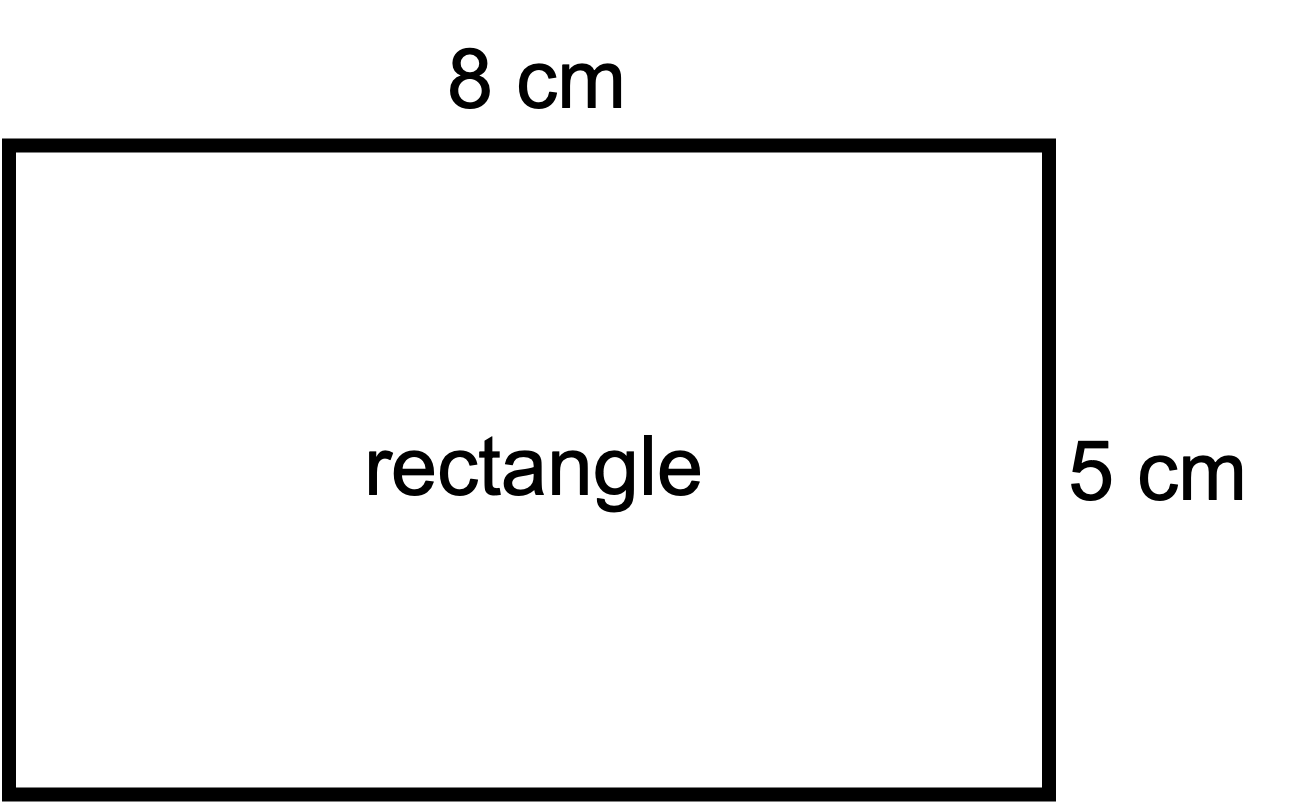
You are told that this shape is a rectangle. What do you know about the lengths of the opposite sides of a rectangle? Do you know the lengths of all the sides now?
Polygon 5
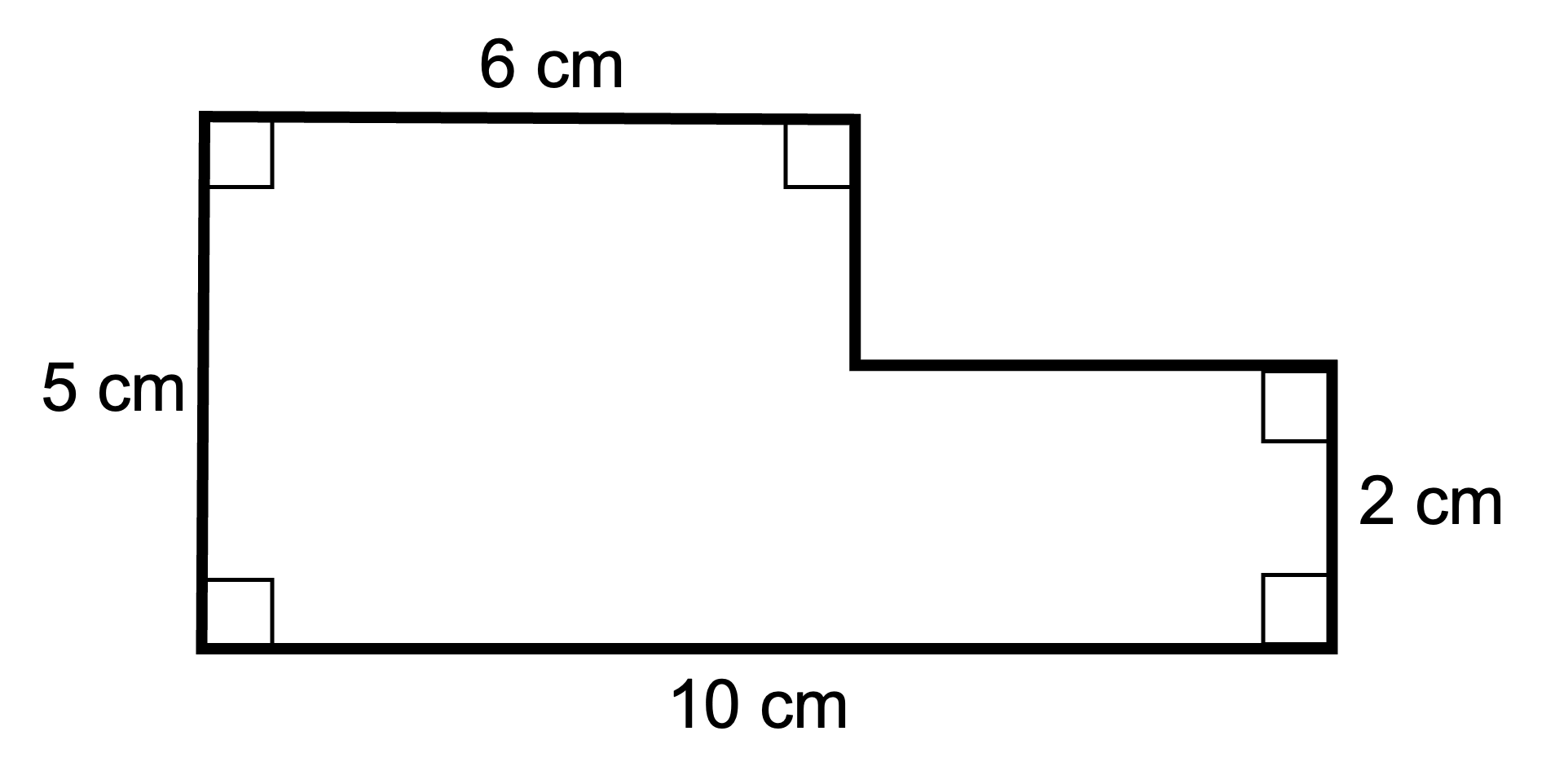
This is an irregular polygon. You have not been given the lengths of all the sides but can you work out what the lengths of the sides you have not been given are?
Answers: You should have gotten the following answers.
- Polygon 1: Perimeter = 17 cm + 16 cm +22 cm +16 cm = 71 cm
- Polygon 2: Perimeter = 9 cm + 7 cm + 3 cm + 8 cm + 4.5 cm + 8 cm = 39.5 cm
- Polygon 3: All three sides are the same length so the perimeter = 6 cm + 6 cm + 6 cm = 18 cm
- Polygon 4: The opposite sides of a rectangle are the same length so the perimeter = 8 cm + 5 cm + 8 cm + 5 cm = 26 cm
- Polygon 5: Here you had to find the length of the missing sides. The one side has a length of 10 cm - 6 cm = 4 cm. The other side has a length of 5 cm - 2 cm = 3 cm. So the perimeter = 6 cm + 3 cm + 4 cm + 2 cm + 10 cm + 5 cm = 30 cm
- Polygon 1: Perimeter = 17 cm + 16 cm +22 cm +16 cm = 71 cm
-
-
-
Perimeter of rectangles and squares
Previously, we worked out what the perimeter of this rectangle was even though we were not given the length of all four sides. We used our knowledge of rectangles to do this.
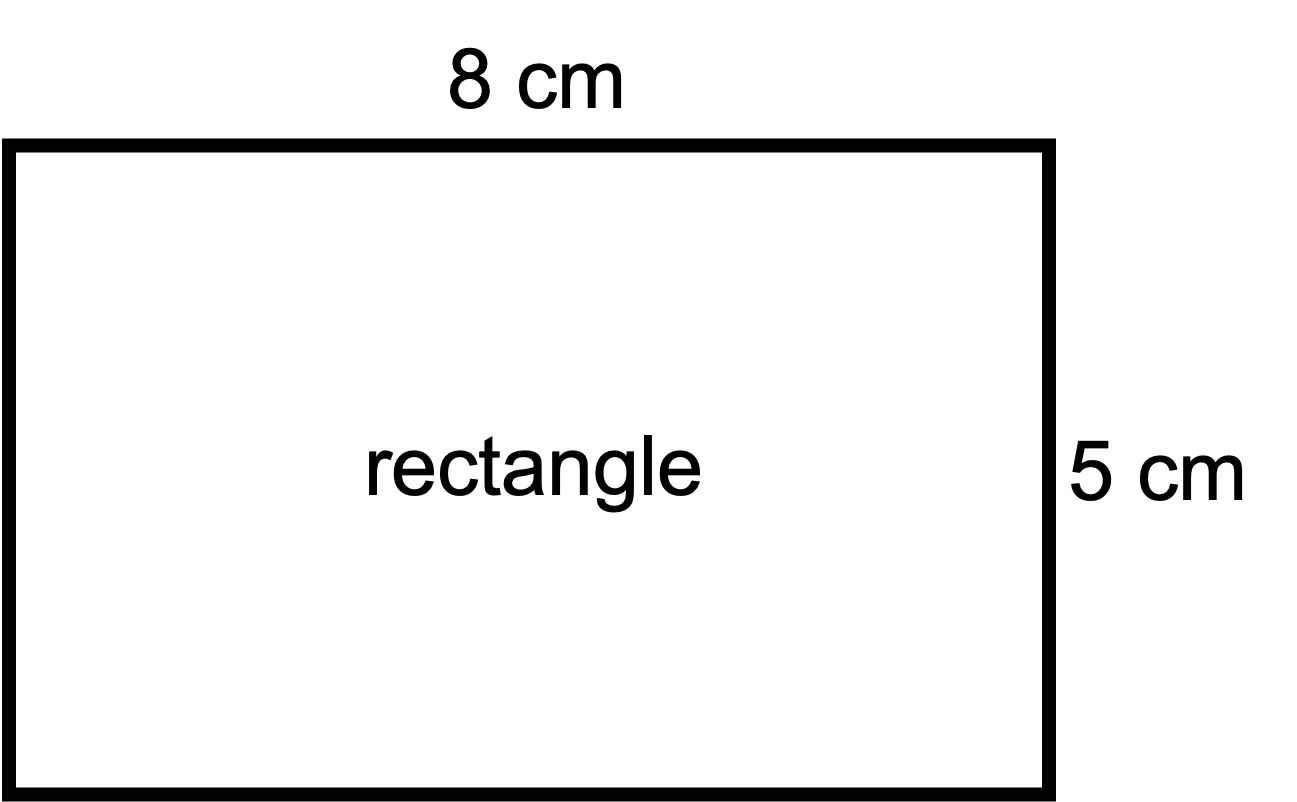
The lengths of the opposite sides of a rectangle are always equal. Therefore, we know that that length of the other two sides are 5 cm and 8 cm. So the perimeter is 5 cm + 5 cm + 8 cm + 8 cm = 26 cm.
Question: Can you think of a simple shortcut we can use to workout the perimeter of any rectangle? Remember, we can label the sides of a rectangle as base and height.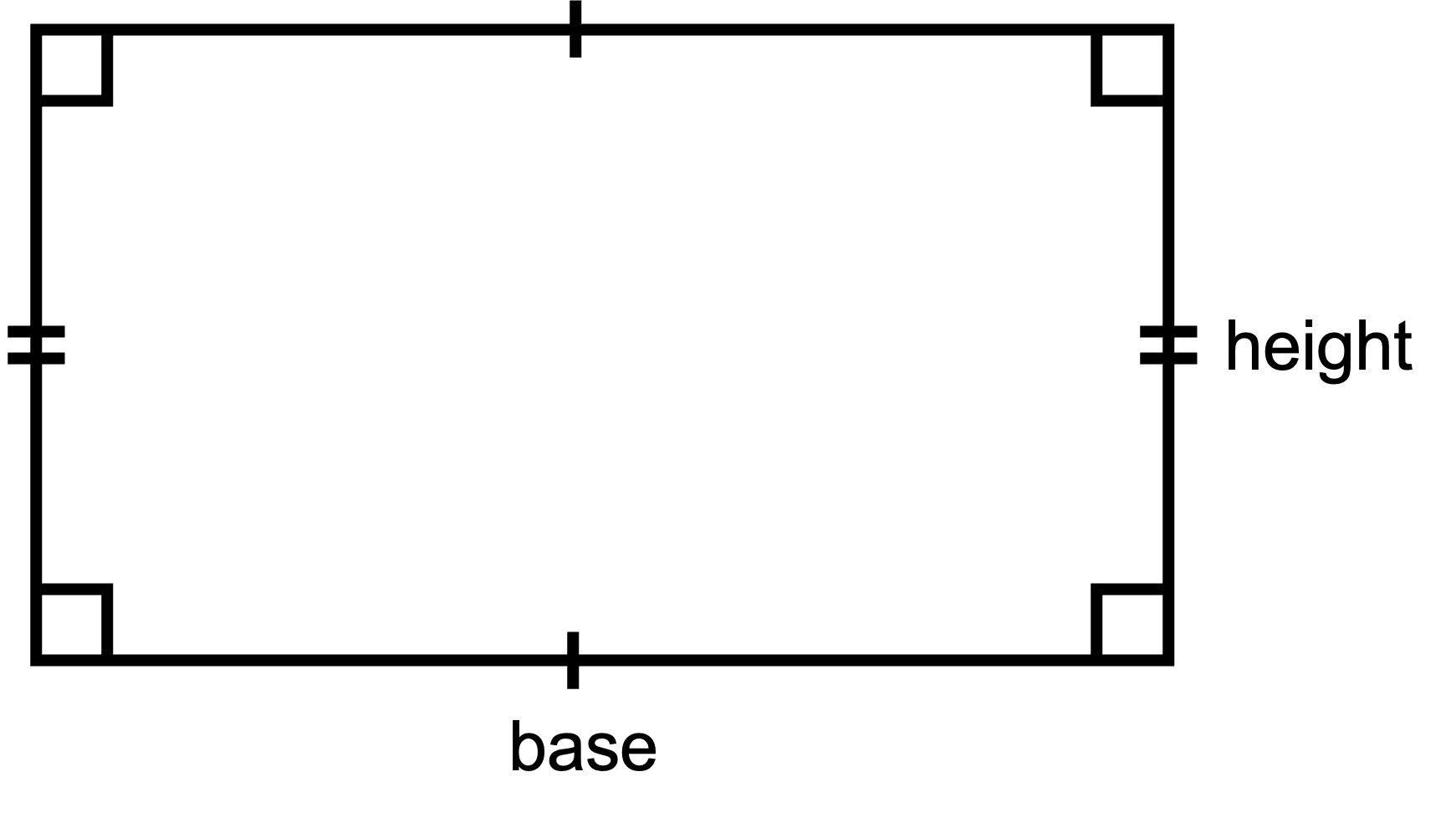
Answer: Well, we know that the perimeter of this rectangle is always going to be base + base + height + height. Why don't we just simplify this to (2 x base) + (2 x height) or 2 x (base + height).
The perimeter of a rectangle can be written as P = 2b + 2h.
Note: Sometimes we call the sides of a rectangle length (the longer sides) and breadth (the shorter sides). In this case we could say that P = 2l + 2b.
Question: Now work out a simple formula for the perimeter of any square. We will call the sides side.
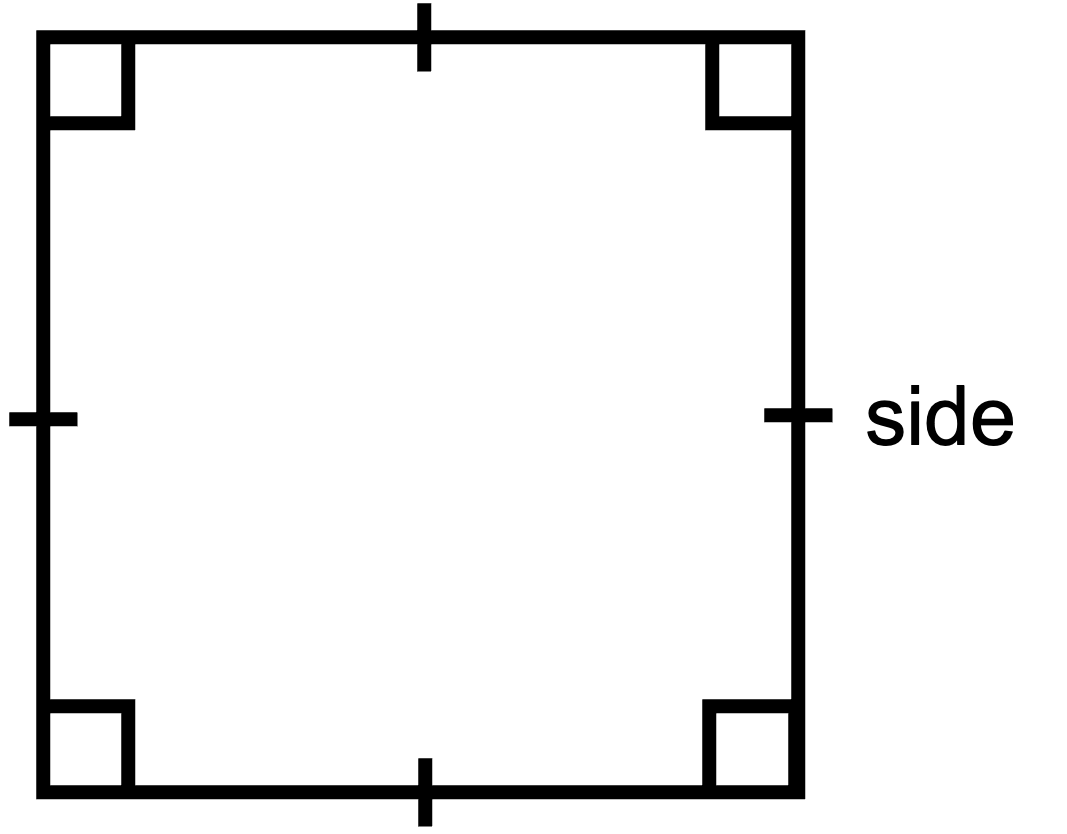
-
Area of rectangles and squares
In the previous section, we saw that we can use shortcuts to find the perimeter of rectangles and squares because we know that the length of the opposite sides of a rectangle are always equal and the length of all four sides of a square are always equal.
- Perimeter of a rectangle = 2b + 2h (base and height) or P = 2l + 2b (length and breadth)
- Perimeter of a square = 4s
Now, let's think about the area of these shapes. We know that area is a measure of the number of square units inside a shape. Look at this rectangle again and count the number of square units inside it.
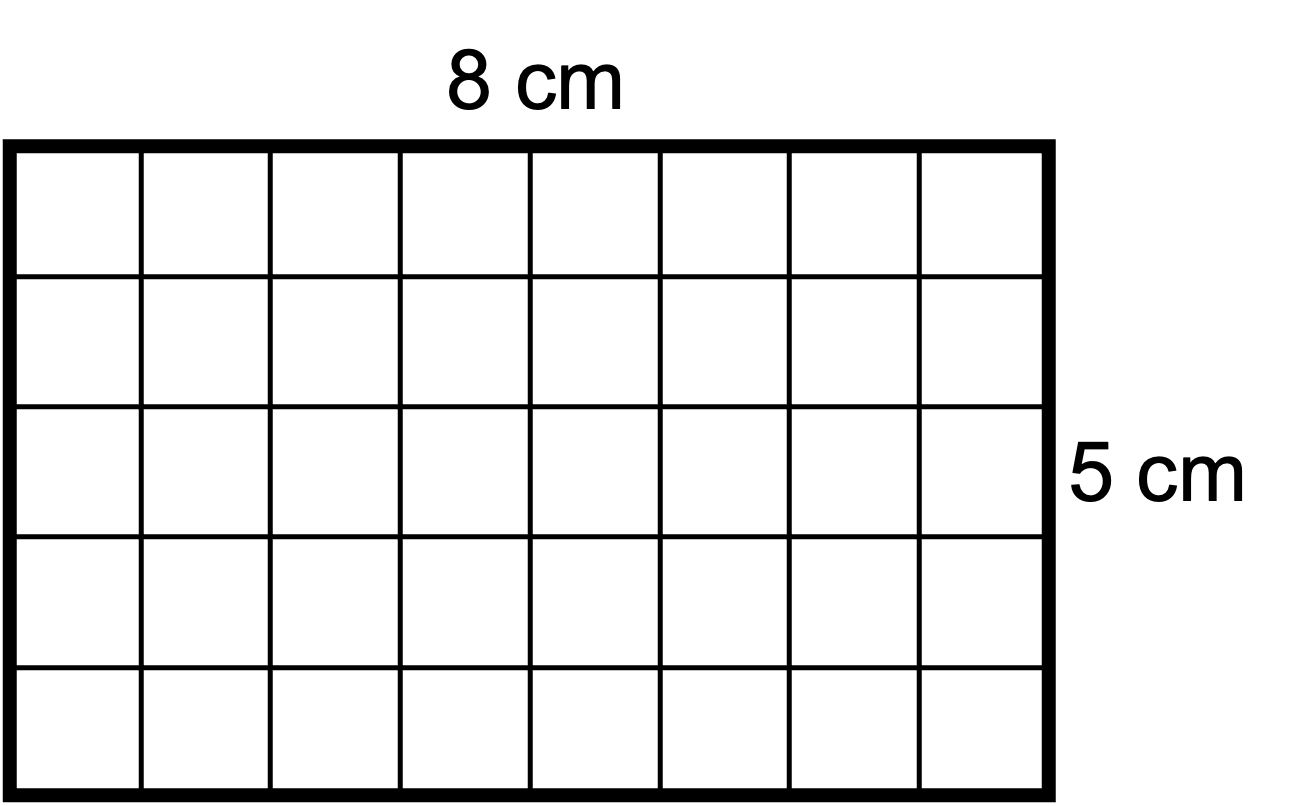
Did you get 40 square centimetres or 40 cm2? Can you see that there are eight rows of five squares (8 x 5) or five rows of eight squares (5 x 8)?
Question: Can you write a simple formula for the area of a rectangle? Remember, we can call the sides the base and height or the length and breadth.
Answer: The area of a rectangle is given as A = b x h (base and height) or A = l x b (length and breadth).
Question: Now work out a simple formula for the area of any square.
- Perimeter of a rectangle = 2b + 2h (base and height) or P = 2l + 2b (length and breadth)
-
Activity: Perimeter and area of rectangles
If you need more help to find the perimeter and area of rectangles and squares, work through the CK-12 FlexBook chapter called Area and perimeter of Rectangles.
-
Activity: Interactive challenge
Work through this interactive challenge from CK-12 to practice finding the perimeter and area of rectangles and squares.
-
Exercise: Challenge question
Raj has a small patch of land that he wants to turn into a vegetable garden. However, he wants to build a fence around it before he plants anything. He knows that the area of the land is 240 m2 and that the length of one side is 1 m longer than the other side.

- What is the perimeter of the vegetable garden?
- If the wood for the fence comes in 2.5 m lengths, how many lengths will Raj need to buy?
This challenge question is based on content from the CK-12 FlexBook called Find Perimeter and Area of Squares and Rectangles Using Formulas.
- What is the perimeter of the vegetable garden?
-
-
-
Perimeter of parallelograms and trapezoids
We have learnt how to find the perimeter and area of rectangles (and squares). We can use this knowledge to help us easily find the perimeter and area of parallelograms and trapezoids.
Think about these 2 shapes. One is a rectangle and the other is a parallelogram that has been created by pushing the rectangle over a bit.
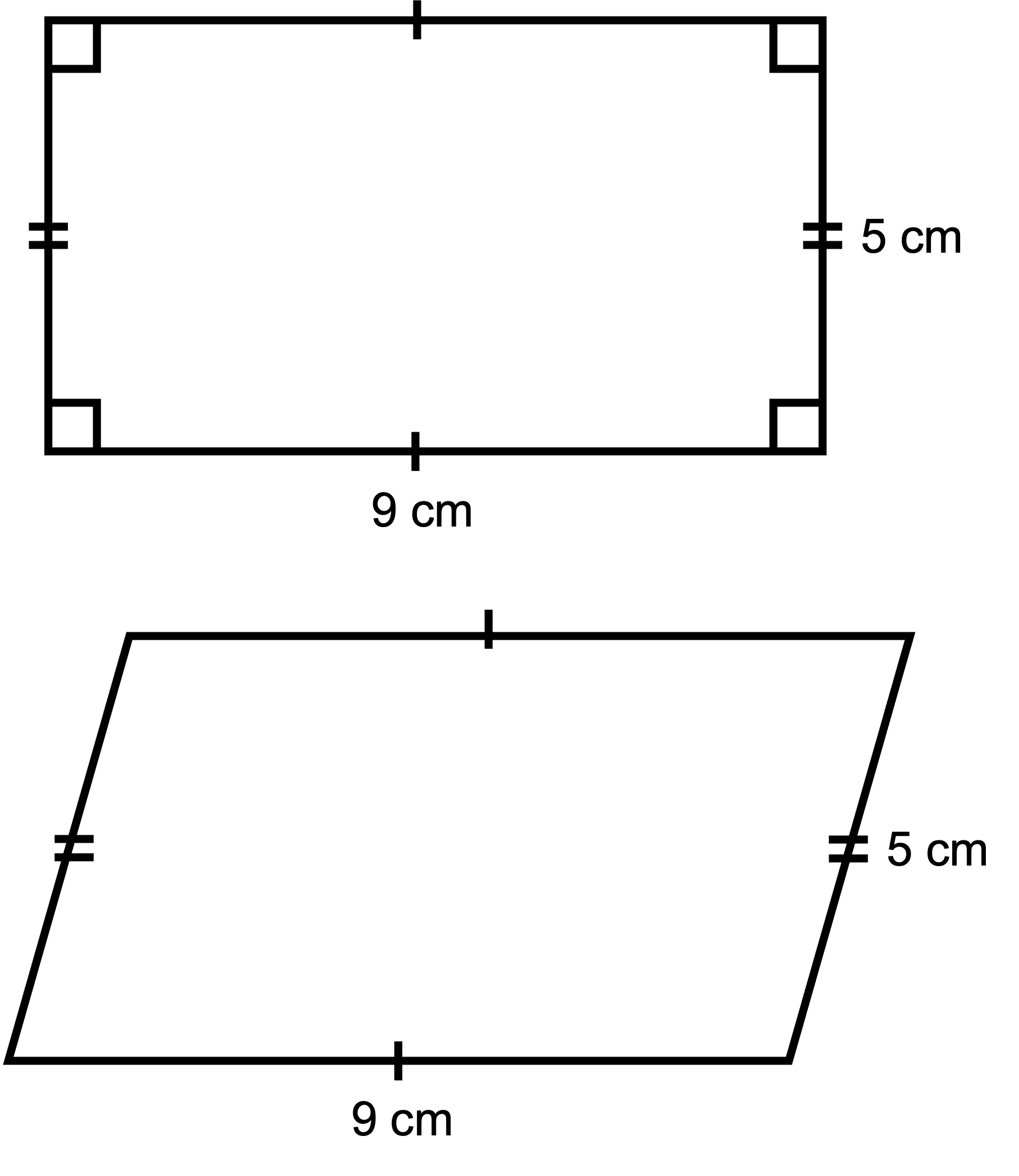
Question: Are the lengths of the sides of the parallelogram still the same? Has the perimeter of the shape changed?
Answer: The lengths of the sides have not changed and the length of the opposite sides of a parallelogram are always equal. Therefore, the perimeter of a parallelogram can be found the same way as the perimeter of a rectangle.
P = 2b + 2h (base and height) or P = 2l + 2b (length and breadth).
But what about a trapezoid? Remember, a trapeziod has only one pair of opposite sides parallel. Because the other two sides are not parallel, they can be different lengths.

If the non-parallel sides happen to be the same length then the shape is a special kind of trapezoid called a trapezium.
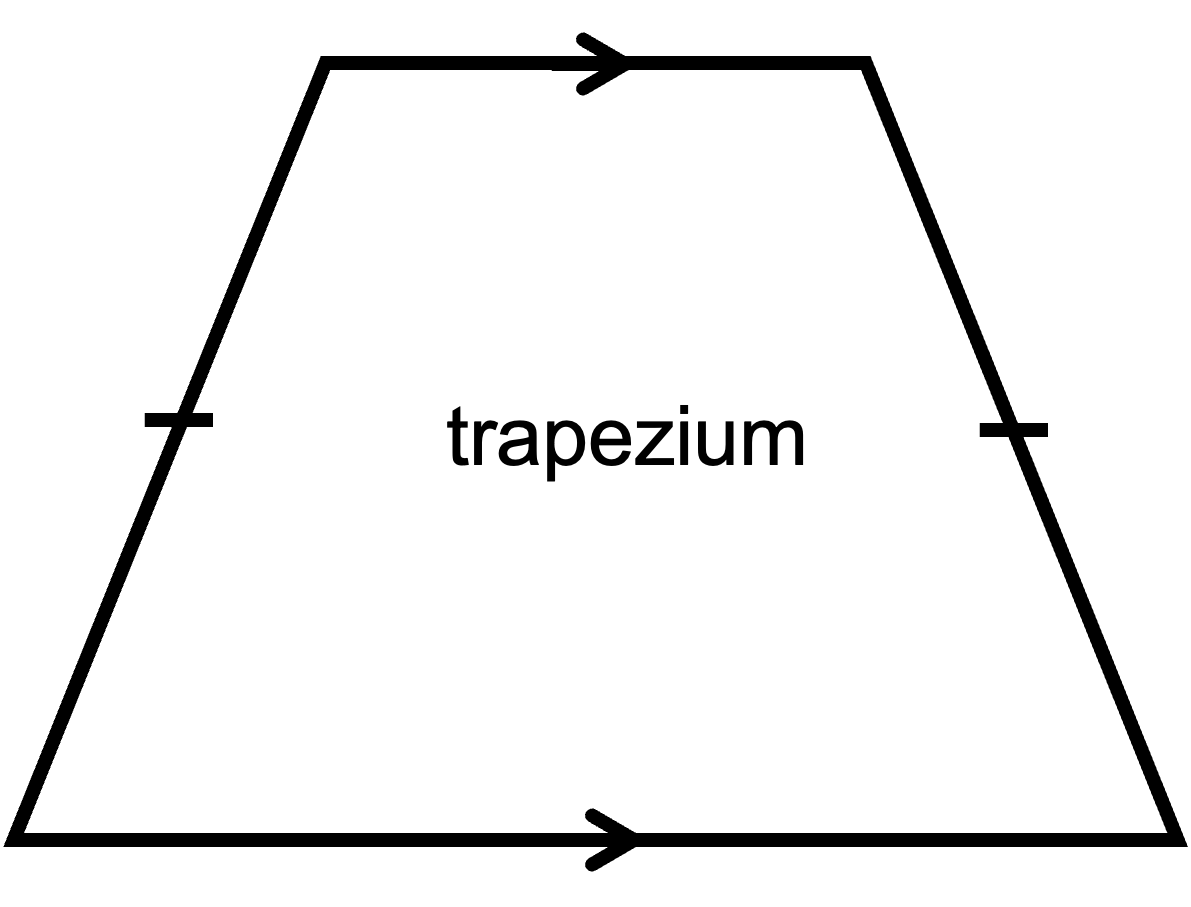
In both cases, it is best to just add up the length of all four sides to find the perimeter.
-
Area of parallelograms and trapezoids
We learnt how to find the area of rectangles (and squares) in the previous section. We can use this knowledge to help us to find the area of parallelograms and trapezoids.
For this activity, you are going to need some blank paper, a ruler, a pencil and a pair of scissors.
Part 1:
1. Draw the following rectangle on your piece of paper. Be as accurate as you can.
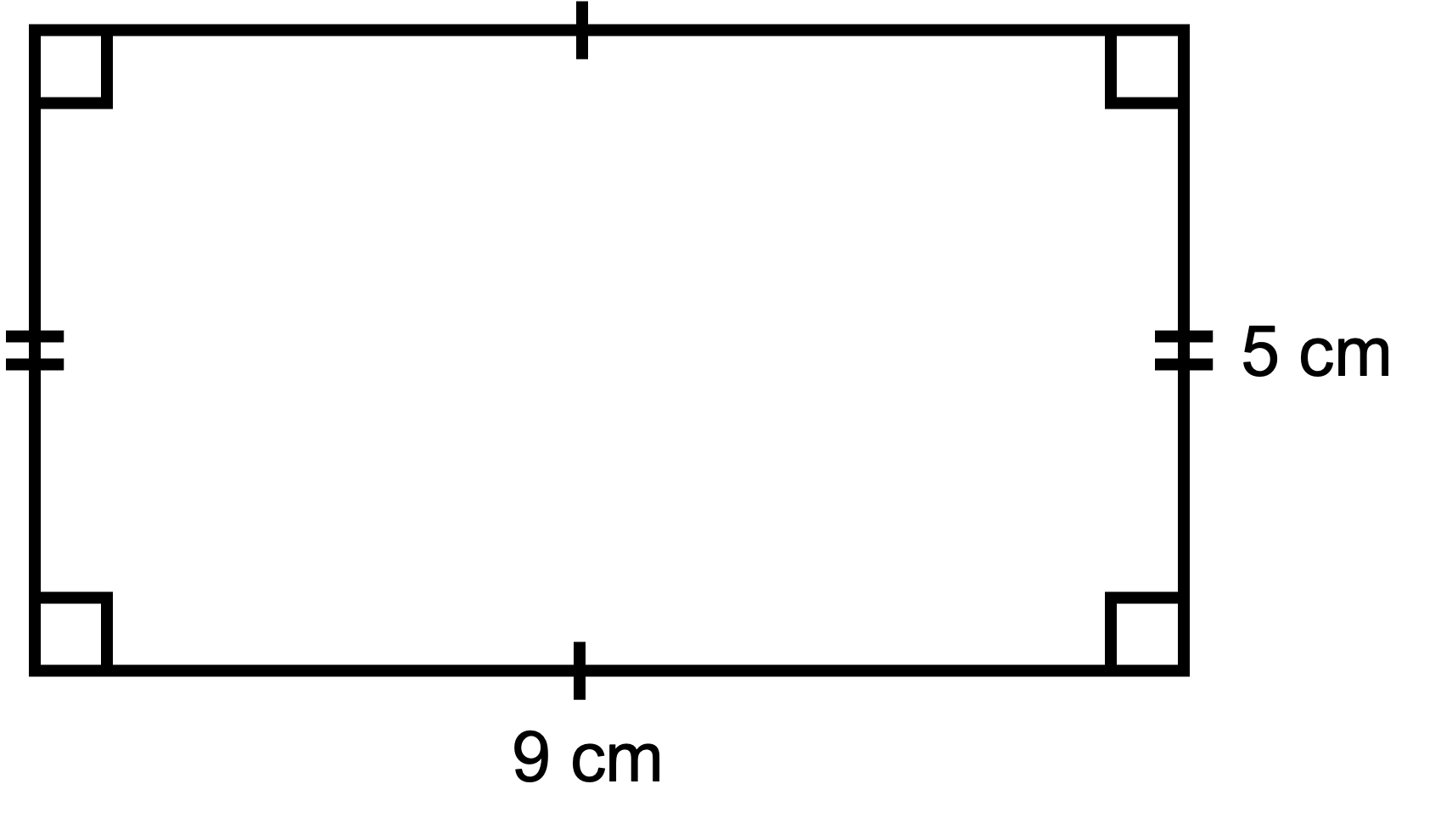
2. What is the area of this rectangle?
3. Cut your rectangle out and then cut a triangle shape off the one end as shown.
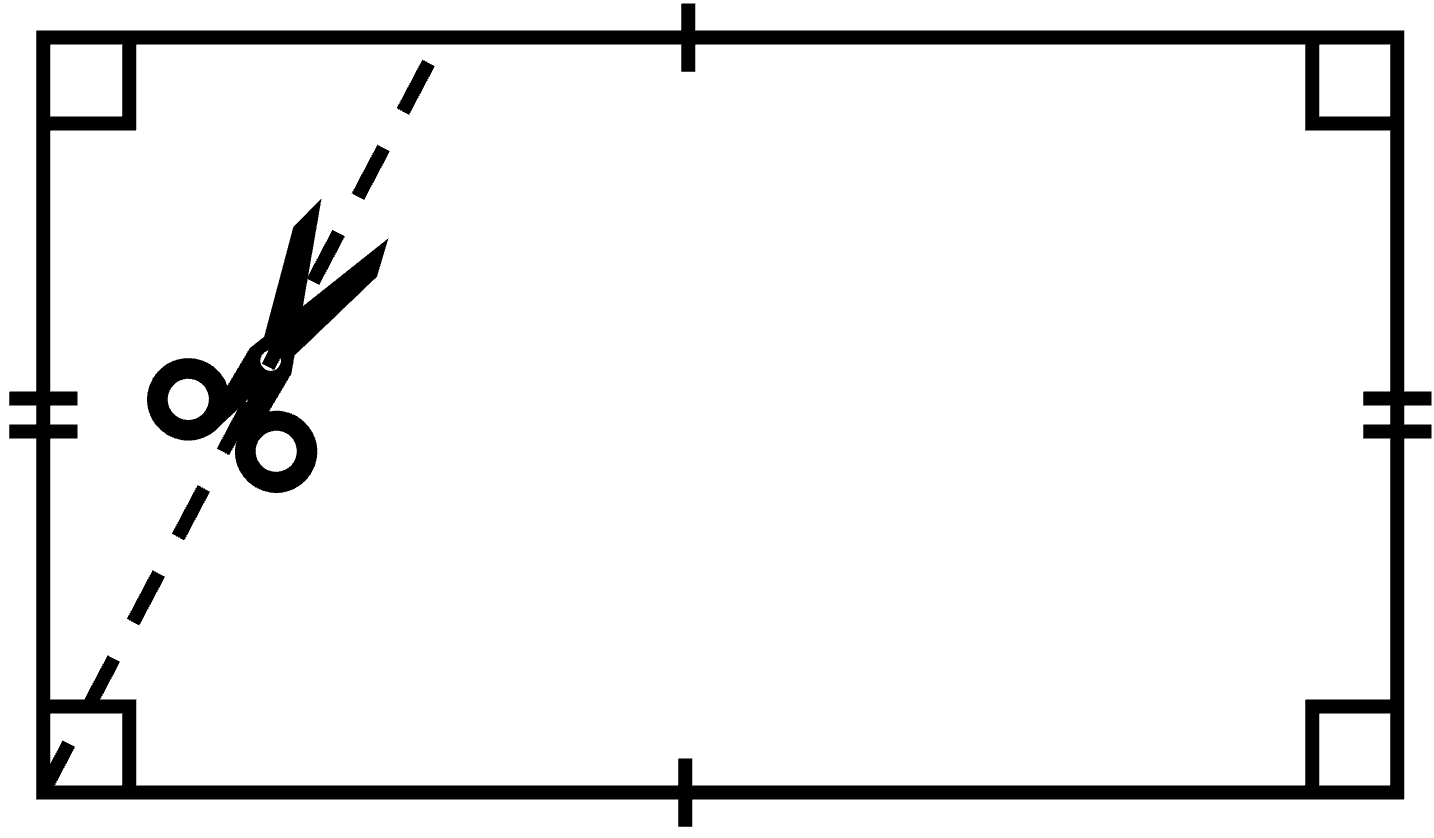
4. Move this triangle over to the other side of the shape. What kind of shape do you create?
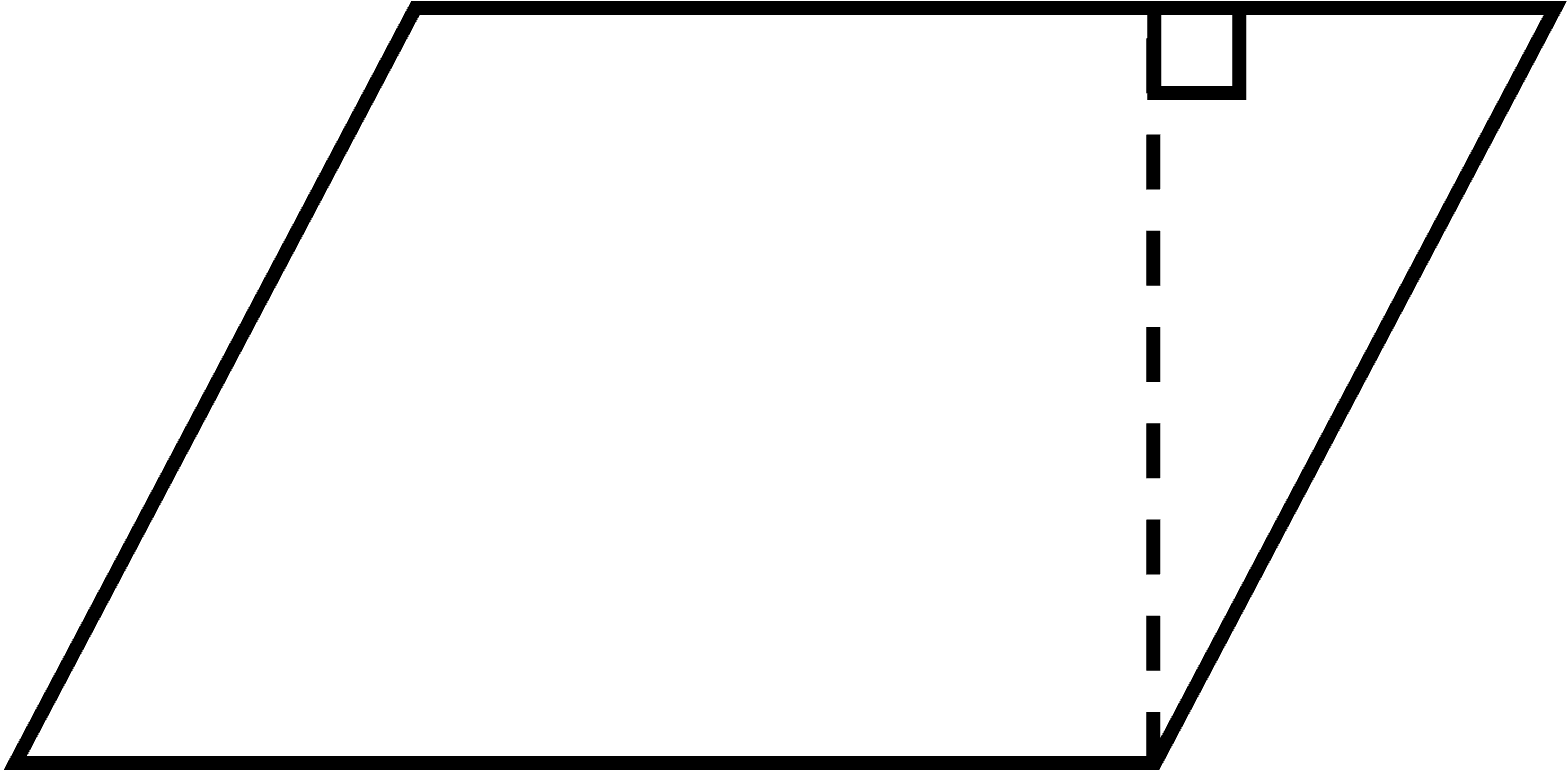
5. Is the area of this parallelogram the same as the area of the original rectangle? How do you know?
7. Will we alway be able to make a parallelogram out of a rectangle like this?
8. What can you say about how to find the area of a parallelogram?
Answer 1:
We can find the area of the original rectangle as A = b x h = 9 cm x 5 cm = 45 cm2.
The area of the parallelogram we created must be the same as the area of the original rectangle because it is made up of the same amount of paper. Therefore, the area of the new parallelogram is also 45 cm2.
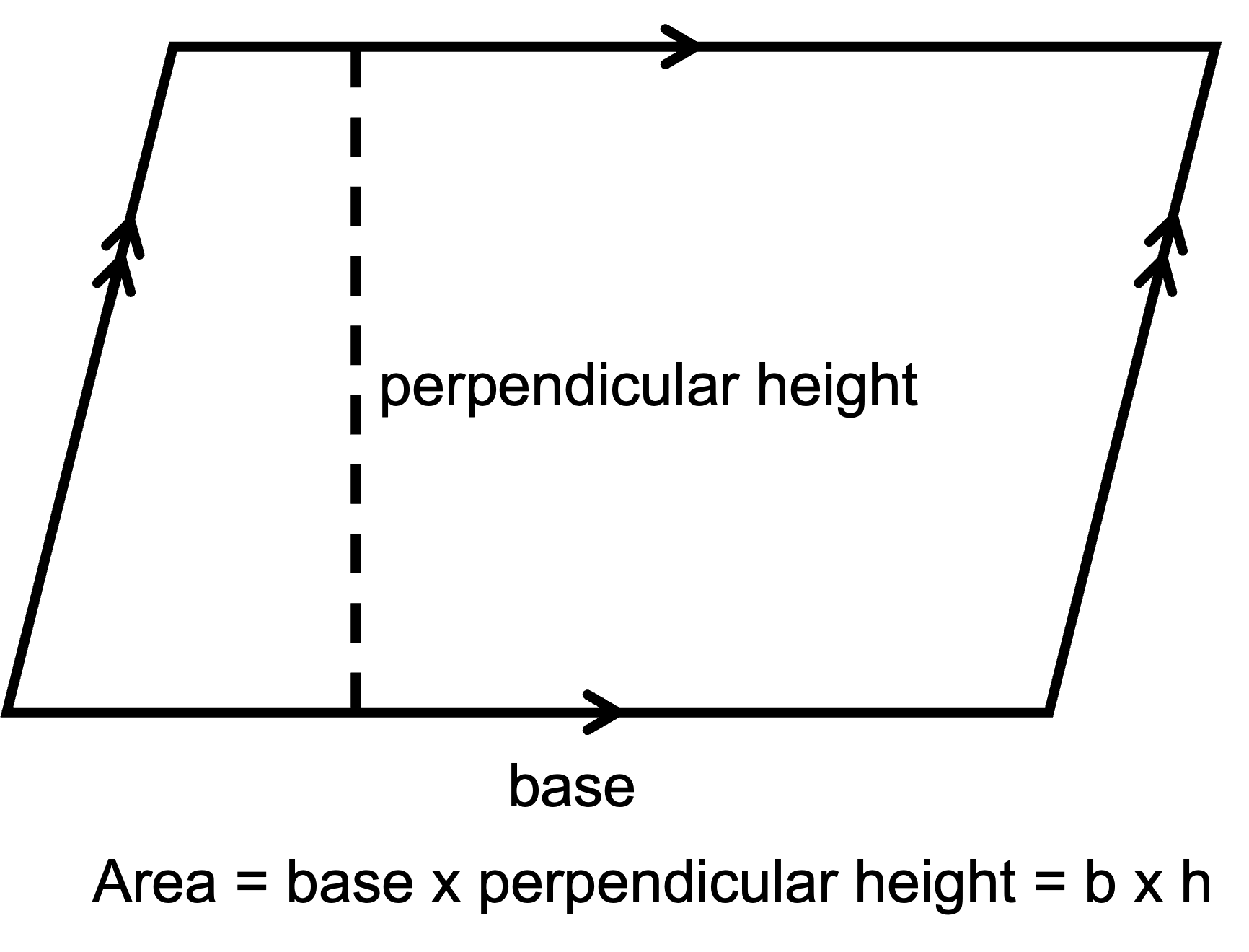
We can calculate the area of any parallelogram as A = b x h.
BUT, h must be the perpendicular height. In other words, it is the distance between the two base sides NOT the length of the other sides.
Part 2:
1. Draw the following trapezoid on your piece of paper. Be as accurate as you can.
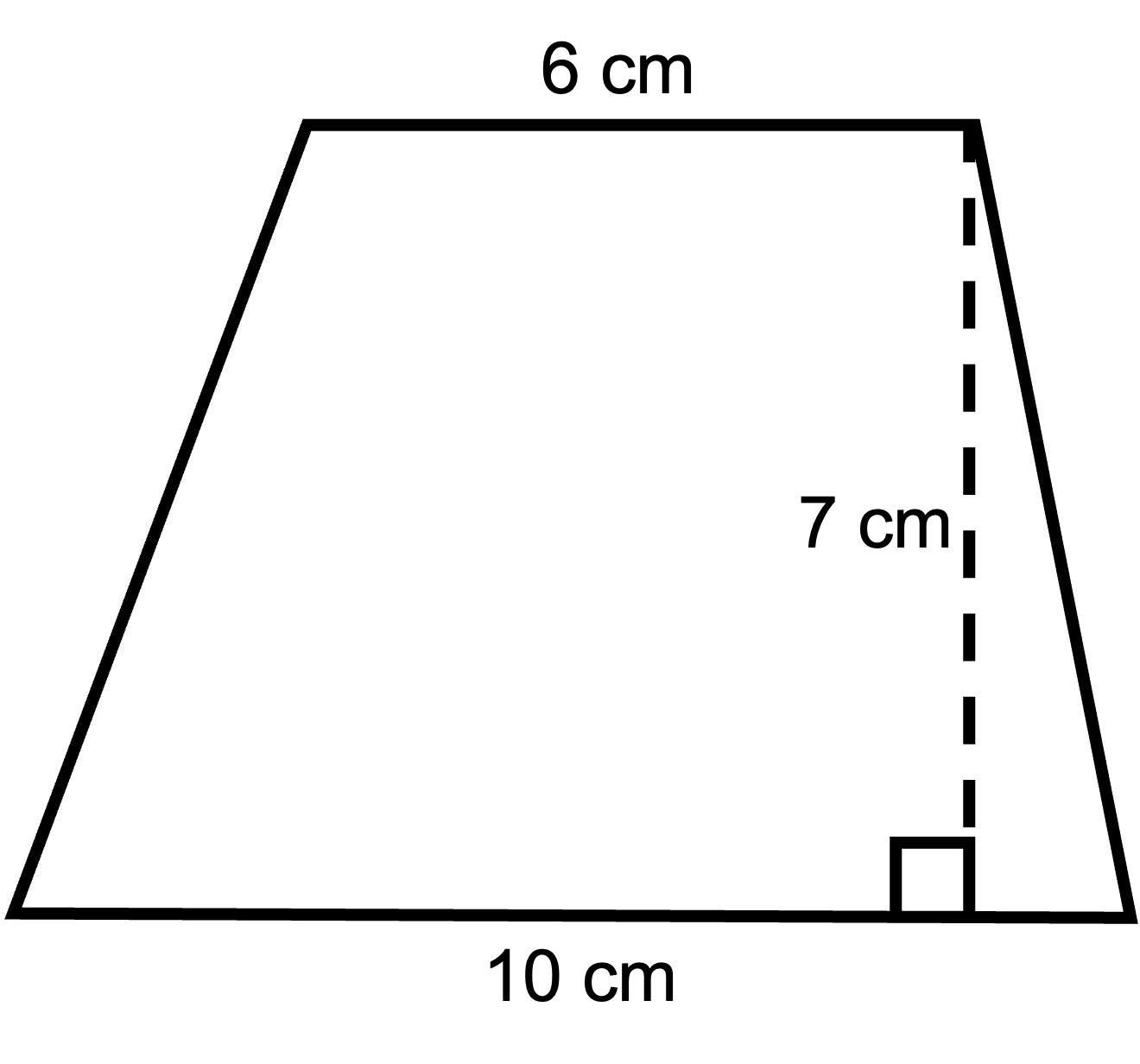
2. Now cut this shape out. Use it as a stencil to cut another copy of this shape out so that you have two identical trapezoids.
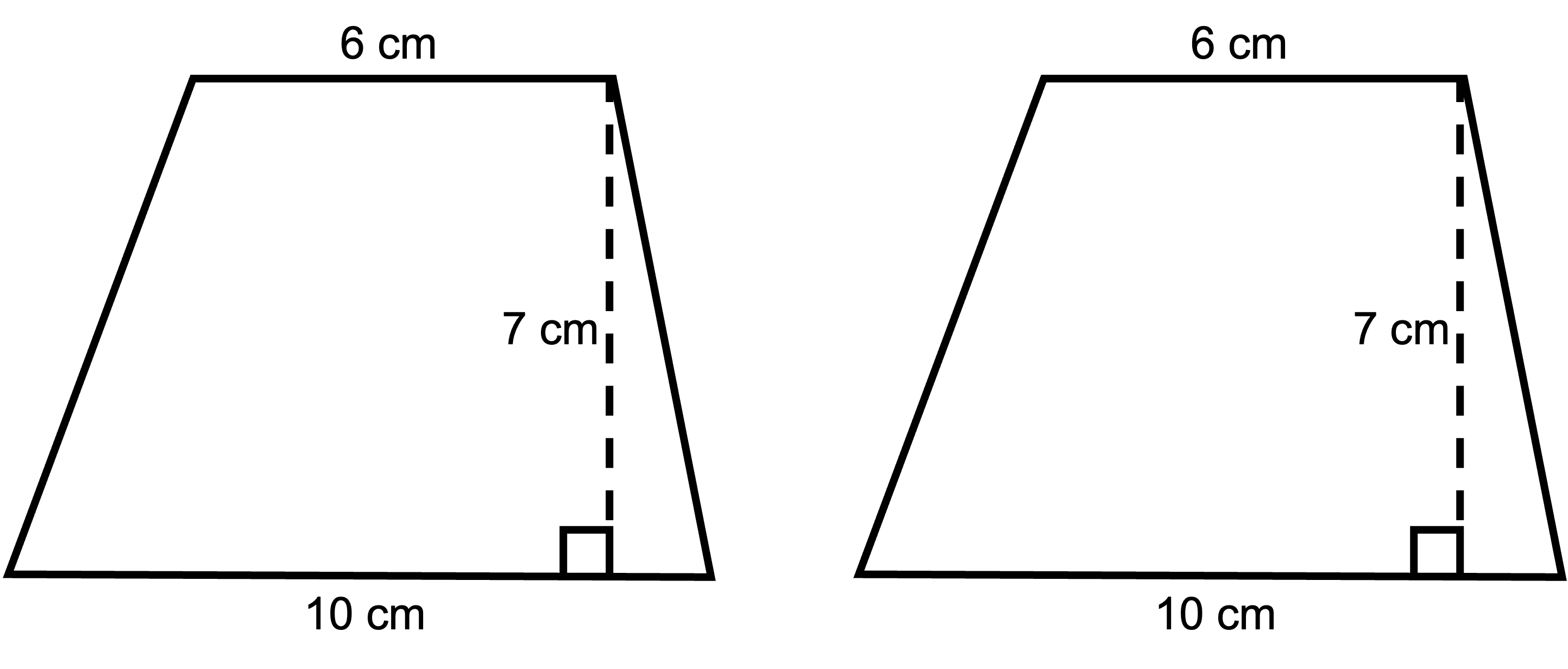
3. Arrange these trapezoids into a parallelogram.
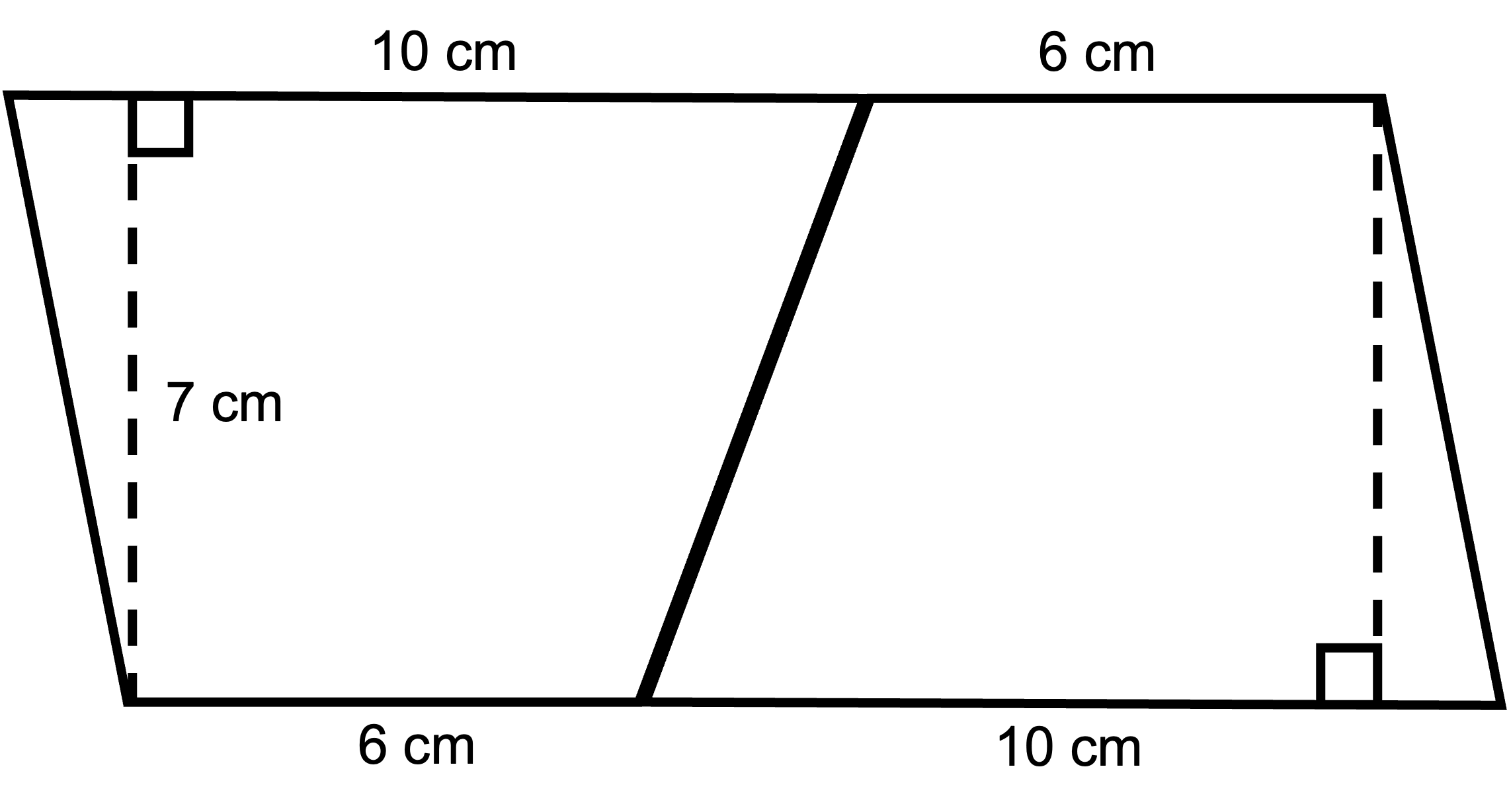
4. What is the area of this parallelogram?
5. How does the area of this parallelogram compare to the area of your original trapezoid?
6. What can you say about how to find the area of a trapezoid?
Answer 2:
The length of the base of the parallelogram you created is 10 cm + 6 cm = 16 cm. Therefore, the area of the parallelogram is A = b x h = 16 cm x 7 cm = 112 cm2.
The area of the original trapezoid is half the area of the parallelogram. But to find the area of the parallelogram we had to add the lengths of the two parallel sides of the original trapezoid.
This means that the area of a trapezoid is
\( \text{Area of trapezoid}=\frac{1}{2}\text{area of parallelogram} \)
\( \text{Area}=\frac{1}{2}\left(\text{base}_1 + \text{base}_2\right)\times \text{perpendicular height} \)
or \( A=\frac{1}{2}\left(b_1 + b_2 \right)\times h \)
-
Activity: Perimeter and area of parallelograms and trapezoids
To learn about finding the perimeter and area of parallelograms and trapezoids, work through the CK-12 FlexBook chapter called Area of Quadrilaterals.
It begins with a refresher of finding the perimeter and area of rectangles (and squares).
-
Activity: Perimeter and area of trapezoids
Get more practice finding the perimeter and area of trapezoids by working through the CK-12 FlexBook chapter called Area and Perimeter of Trapezoids.
-
Activity: Interactive challenge
Work through this interactive challenge from CK-12 to practice finding the perimeter and area of rectangles and squares.
-
-
-
Area of triangles
We already know how to find the perimeter of any triangle. We add the lengths of the three sides. But how can we easily find the area of a triangle?
1. Look at the shape below. ABCD is a parallelogram. What is the area of ABCD?
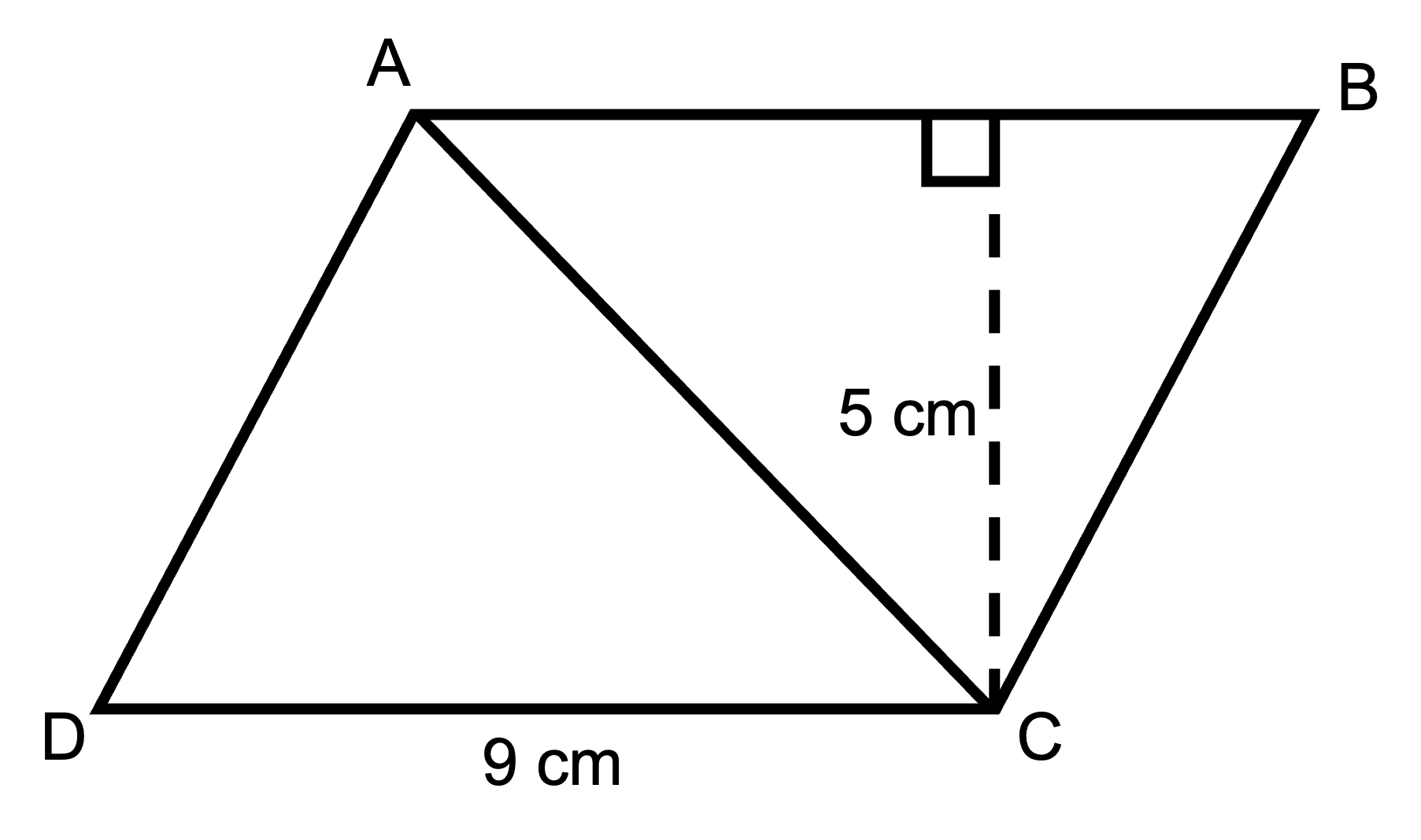
2. What shape is ABC? What is the area of ABC? How do you know?
3. What can you say about how to find the area of any triangle?
Answer:
The area of parallelogram ABCD is A = b x h = 9 cm x 5 cm = 45 cm2.
ABC is a triangle. Its area is exactly half the area of the parallelogram. We have cut the parallelogram in half to create triangle ABC. Therefore, the area ABC is 22.5 cm2.
We can always cut a parallelogram into two identical triangles. We can also arrange two identical triangles into the shape of a parallelogram. This means that the area of a triangle is always half the area of the parallelogram we could make from two of these triangles.
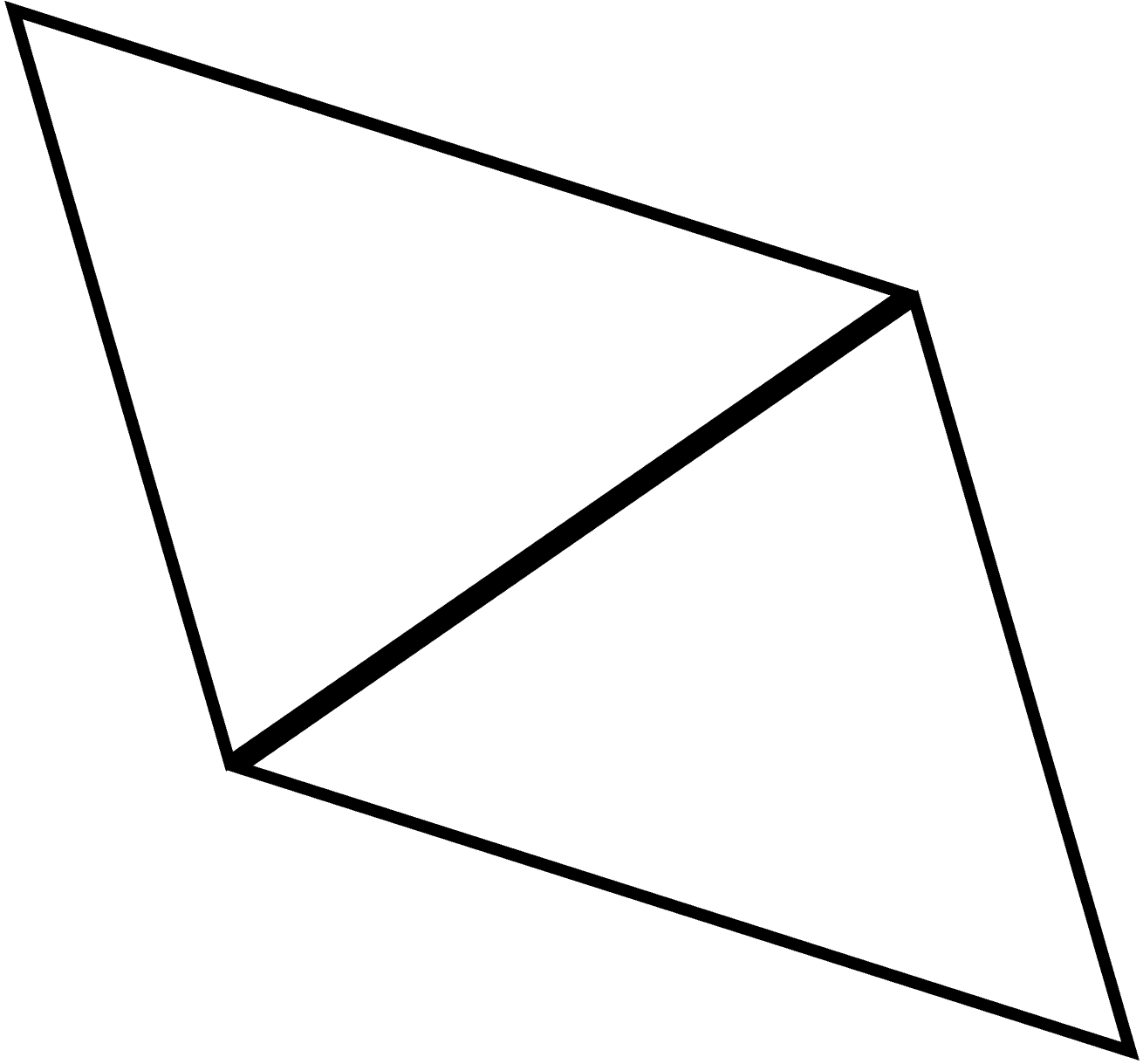
In other words, the area of a triangle is \( \text{area of triangle} = \frac{1}{2}\text{area of parallelogram} \)
\( A=\frac{1}{2}\left(\text{base}\times \text{perpendicular height}\right) \)
\( A=\frac{1}{2}bh \)
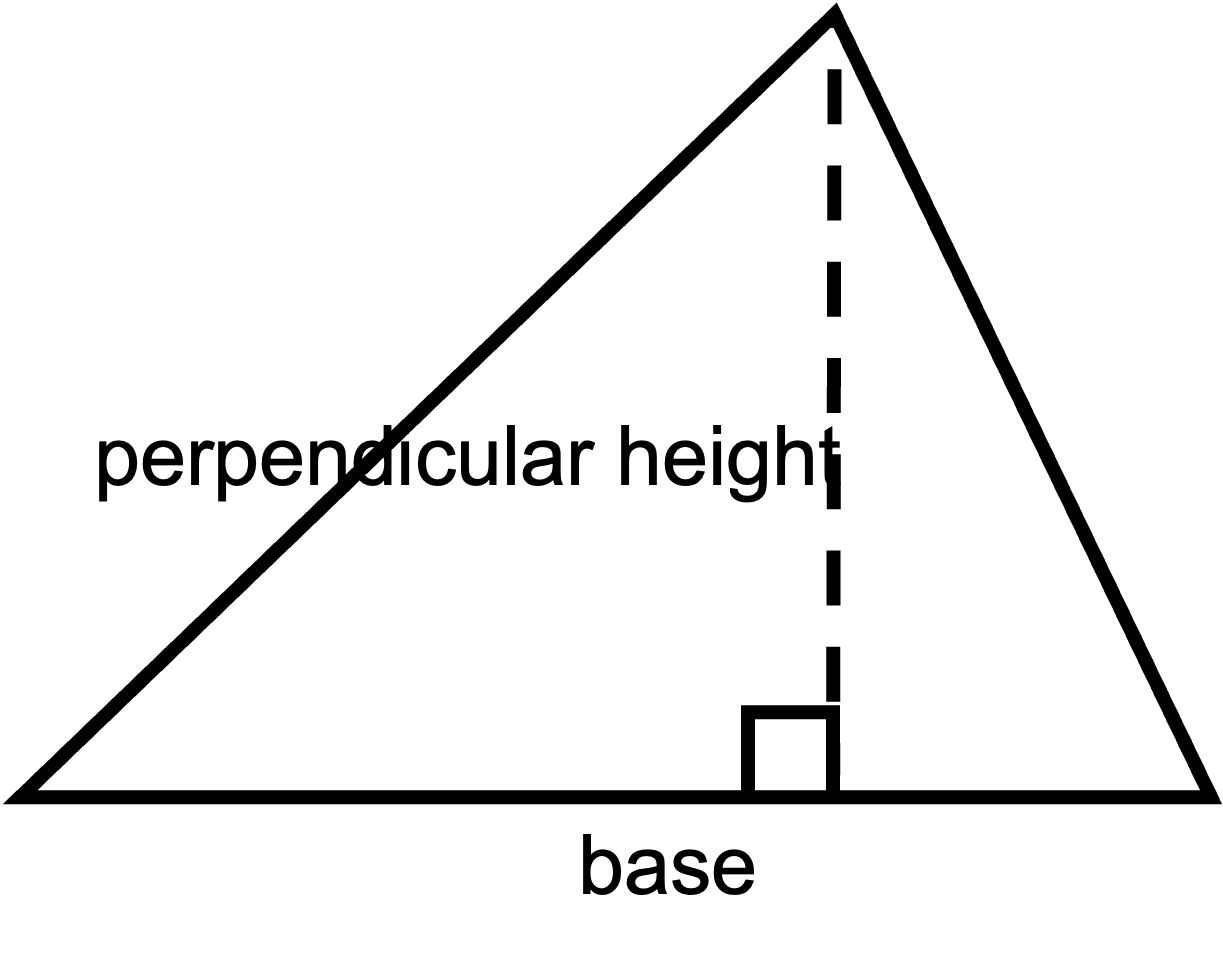
Learn more by working through the CK-12 FlexBook chapter called Area of Triangles.
-
-
-
The circle
Circles are very special shapes. They have no straight edges. Instead they are defined by every point on the circle being exactly the same distance from a single point, the centre. This distance is called the radius (r).
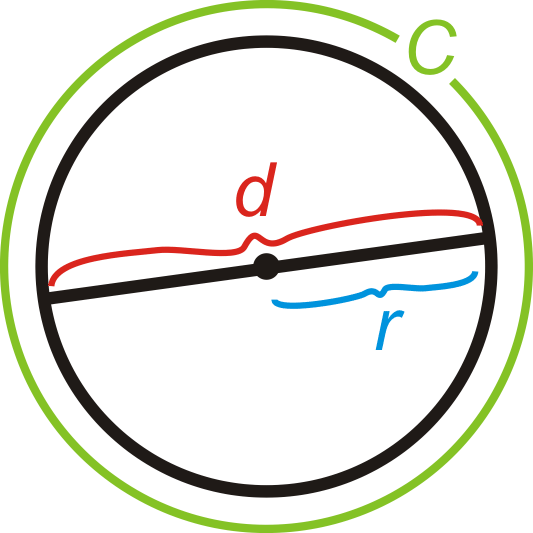
The diameter (d) of a circle is the straight line that passes from one side of the circle to the other through the centre. Therefore it is twice the length of the radius.
Because circles are so special, we give their perimeter a special name - the circumference (C).
-
What is Pi?
Before we learn about how to find the circumference and area of circles, we need to know one more thing that makes circles so special.
If you measure the diameter and circumference of any circle, it turns out that the ratio of the length of the circumference to the length of the diameter is always the same value, about 3.14. This is a very special number which we call\( \pi \) /(pi).
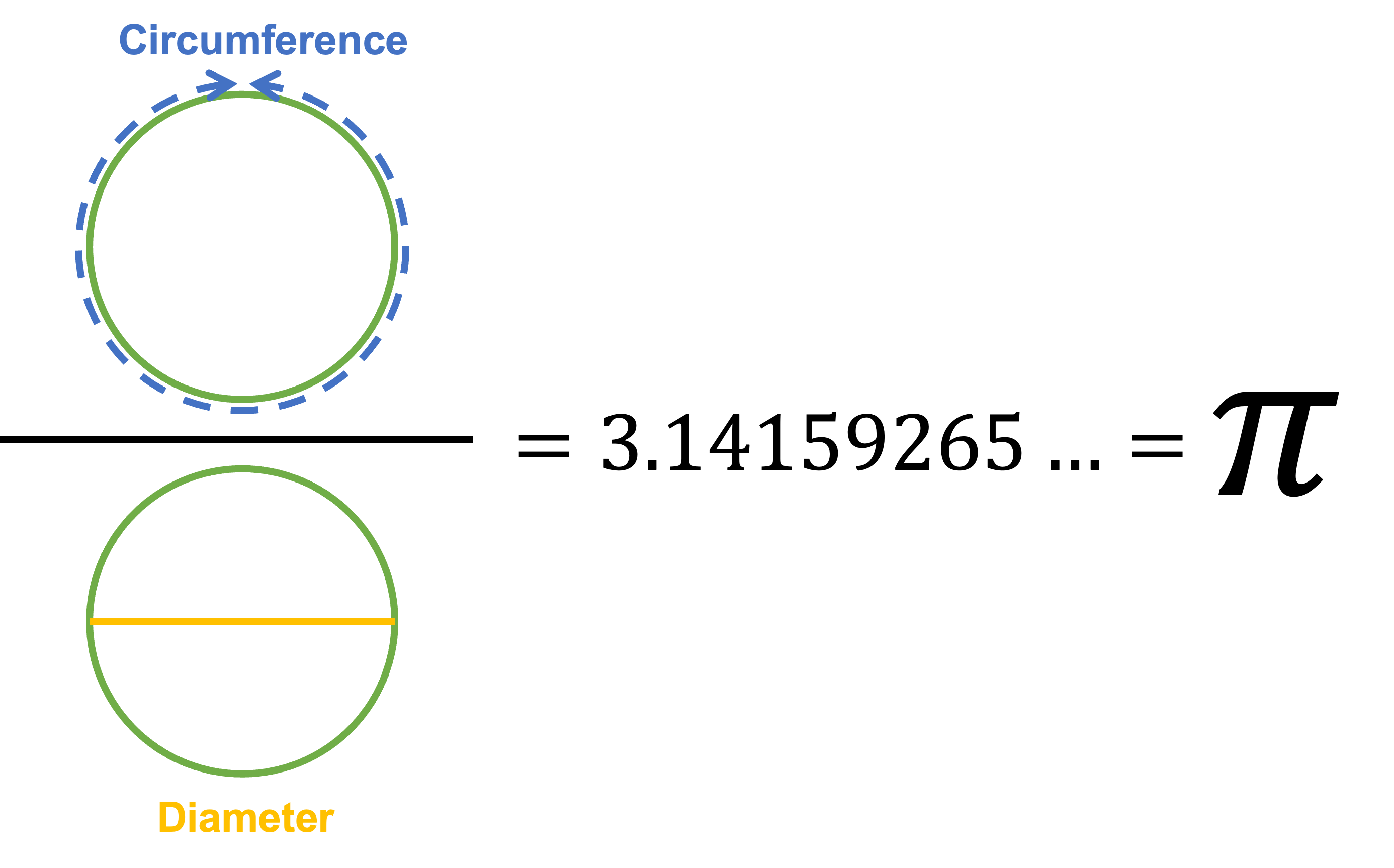
Watch this Animation of Pi (with narration) (1:11) for an excellent visual explanation.
-
Activity: Interactive challange
Work through this interactive challenge from CK-12 to practice working with \( \pi \) and the diameter and radius of a circle.
-
Activity: Circumference of a circle
To learn how to find the circumference of a circle by working through this CK-12 FlexBook chapter called Circumference.
-
Activity: Area of a circle
To learn how to find the area of a circle work through the CK-12 FlexBook chapter called Area of a Circle.
Now watch this example of finding the area of a circle.
-
Activity: Interactive challenge
Work through this interactive challenge from CK-12 to practice finding the area of circles.
-
