Sectieoverzicht

    • Leerlingen moeten
      Als voltooid aanduiden

      Elastic and inelastic collisions

      Momentum, kinetic energy and impulse can be used to analyse collisions between objects such as vehicles or balls. Forces and the final velocity of objects can be determined.

      Elastic vs inelastic collision is a comparison of two types of collisions that differ in the conservation or loss of kinetic energy.

      In an elastic collision, the total kinetic energy of the colliding objects is the same before and after the collision. In an inelastic collision, the total kinetic energy of the objects is less after the collision than before, and some energy is changed into other forms like heat, sound, or radiation.

      Another way to distinguish elastic and inelastic collisions is by looking at whether the objects are stuck together or moving separately before and after the collision. If the objects are stuck together either before or after the collision, the collision is inelastic; if the objects start and end moving separately from each other, the collision is elastic.

      If kinetic energy before is the same as after, then the collision is elastic. Interactions between molecules are examples of perfectly elastic collisions. In most other cases (eg snooker balls), collisions are not perfectly elastic - some kinetic energy is lost. But this must be tested by calculation.

      Kinetic energy can be calculated using the following equation:

      Ek = 1/2 mv2

      When working with collisions, kinetic energy must be worked out for each object involved both before and after the collision.

      Question:

      If two bumper cars collide head-on in a fairground and both cars come to a stop due to the collision, kinetic energy is obviously not conserved. Is momentum conserved even though both cars stop?

      Answer:

      Yes, although there is no momentum after the collision, there was no total momentum before the collision. Momentum is a vector quantity. The positive momentum of one car must have been balanced out by the negative momentum of the other car.

      Question:

      Is kinetic energy conserved even though both cars stop?

      Answer:

      No. Kinetic energy is a scalar quantity so there is no balancing out of the different directions. Both cars were moving and had kinetic energy before the collision. Both cars are at rest and have no kinetic energy after.


      Question
      A red snooker ball and a blue snooker ball (each with a mass of 160 g) collide. The red ball is travelling from left to right at 0.28 m/s. The blue ball is travelling from right to left at 0.12 m/s. This is shown in the diagram below.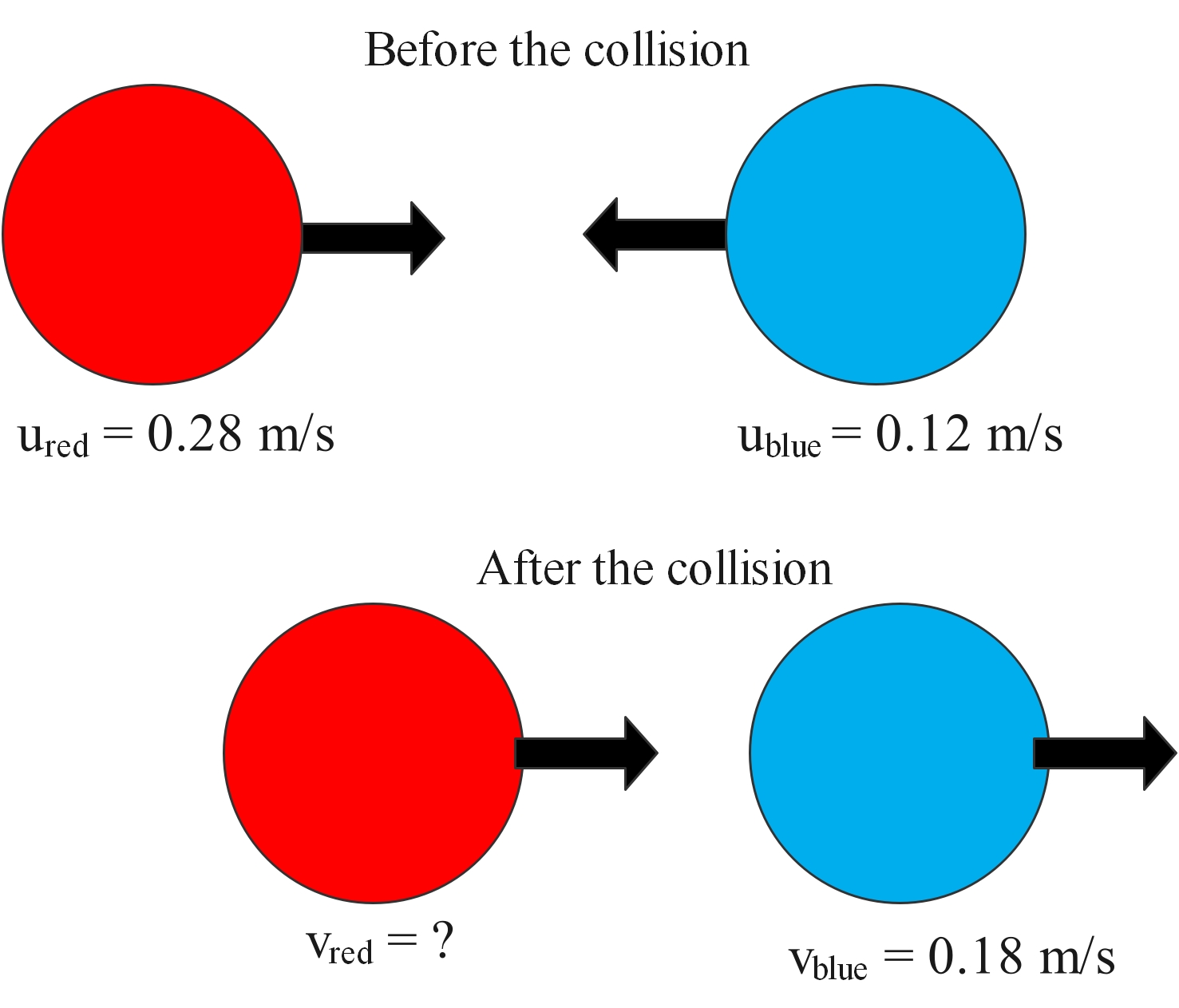
      snooker balls

      After the collision, the blue ball travels from left to right at 0.18 ms-1.

      a) Calculate the velocity of the red ball after the collision.
      b) Use kinetic energy to determine whether the collision was elastic or not.

      Answer:
      a) Total momentum before = total momentum after
      mredured + mblueublue = mredured + mblueublue

      0.16 × 0.28 + 0.16 × (−0.12)= 0.16× vred + 0.16 × 0.18

      Rearranging:

      0.16× vred   =(0.0448−0.0192) − 0.0288

      =0.0256−0.0288

      =−0.00320.16

      vred =−0.02 m/s. This is a negative value, so the direction is from right to left.

      b) To determine if the collision is elastic or not, you must work out the kinetic energy before and after the collision.
      This example deals with two objects. The kinetic energy before the collision involves their initial speed.  
      The kinetic energy before the collision is 0.00742 J
      The kinetic energy after the collision is 0.00262 J
      So the total kinetic energy lost is 0.0048 J
      The collision is inelastic. 


    • Leerlingen moeten
      Als voltooid aanduiden

      Linear Momentum

      Momentum

      Momentum is the product of a moving object's mass and velocity.

      Momentum = mass x velocity

      The symbol for momentum is p

       so this can also be written as: p = mv

      Momentum is measured in kg ms-1.

      Momentum is a vector quantity that depends on the direction of the object. Momentum is of interest during collisions between objects.

      When two objects collide the total momentum before the collision is equal to the total momentum after the collision (in the absence of external forces).

      This is the law of conservation of momentum. It is true for all collisions.

      Conservation of momentum example

      Consider two model cars of mass 1.2 and 1.4 kg colliding at the speeds shown:

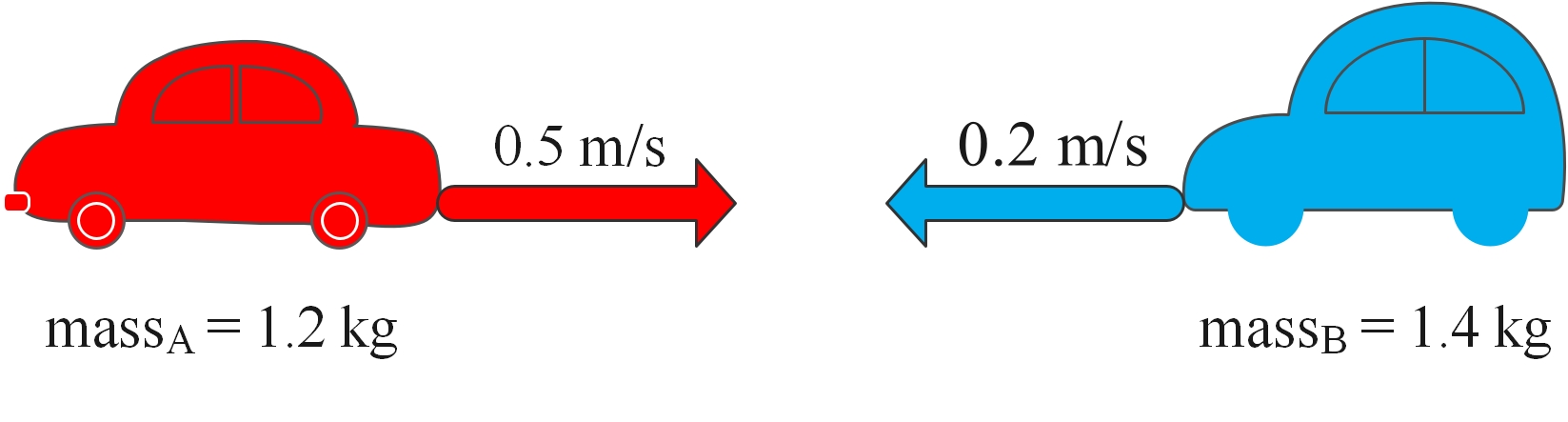
      cars momentum

      The total momentum before the collision is the sum of both momentums:

      Momentum of red car A:

      p = mAv
      1.2 x 0.5
      = 0.6 kg m/s

      Momentum of red car B:
      p = mBv
      1.4 x 0.2
      = 0.28 kg m/s

      The blue car is travelling in the negative direction, so the momentum is subtracted.

      Total momentum:

      0.6 - 0.28

      = 0.32 kg m/s

      If the two cars stick together after the collision and move as one, then the velocity of the two cars can be determined because the total momentum after the collision is the same (ie 0.32 kg m/s).

      The total mass is now 2.6 kg.

      Total momentum after collision is 0.32 kg m/s:

      0.32 = mAB x vAB  

      0.32 = 2.6 x vAB  

      vAB  = 0.32/2.6

      = 0.12 m/s

      The velocity is positive, so this shows that the two cars move off in the positive (left to right) direction.

      • The total momentum of two objects before a collision is the same as their total momentum after the collision - provided there are no external forces.
      • Momentum is conserved in a collision, but kinetic energy is not.
      • Momentum (kg m/s) = mass (kg) x velocity (m/s).  It is a vector quantity
      • Principle of conservation of momentum:                                                                total momentum before collision = total momentum after collision



    • Linear momentum Test
      Leerlingen moeten
      Als voltooid aanduiden