Sectieoverzicht
-
-
Leerlingen moetenAls voltooid aanduiden
Force, mass and acceleration
When the forces on an object are unbalanced, there is a resultant force. This resultant force cause the object to change its velocity. It will accelerate or decelerate.
The bigger the force on the object, the more it accelerates.
The heavier the object, the less it accelerates.
Newton's second law of motion can be described by this equation:
resultant force = mass × acceleration
F = ma
This is when:
- force (F) is measured in newtons (N)
- mass (m) is measured in kilograms (kg)
- acceleration (α) is measured in metres per second squared (m/s2)
The equation shows that the acceleration of an object is:
- proportional to the resultant force on the object
- inversely proportional to the mass of the object
In other words, the acceleration of an object increases if the resultant force on it increases, and decreases if the mass of the object increases.
One newton (1 N) is defined as the force which gives to a mass of 1 kg, an acceleration of 1 m/s2.
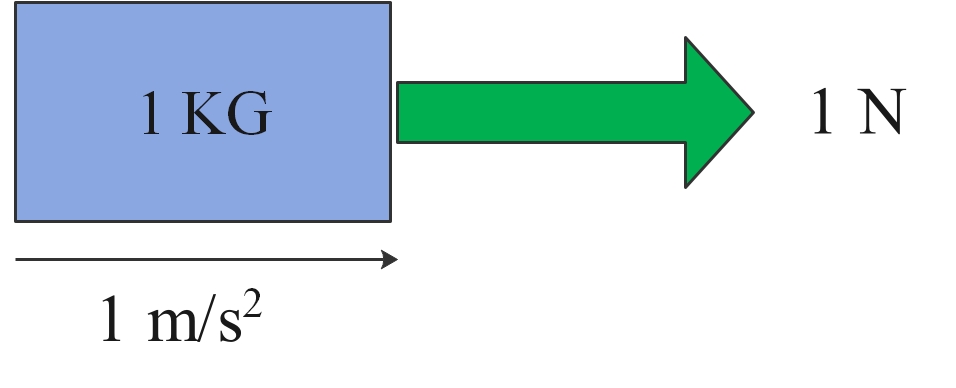
Example:
Calculate the force needed to accelerate a 22 kg cheetah at 15 m/s2.
F = 22 x 15
F = 330 N
Example:
Calculate the force needed to accelerate a 15 kg gazelle at 10 m/s2.
F = ma
F = 15 x 10
F = 150 N- Newton's second law: Force = change in momentum/time taken = rate of change of momentum
-
Leerlingen moetenAls voltooid aanduiden
Investigating acceleration
Investigate the relationship between the force, mass and acceleration by varying the masses added to trolleys
More than one method could be used to investigate the relationship between the force, mass and acceleration. This method will vary the masses added to trolleys.
Aim of the experiment
To investigate the relationship between the force, mass and acceleration by varying the masses added to trolleys.
Method
The video shows apparatus that can used in this investigation.
- Set up the equipment. Make sure that the track is level, and that the card will pass through both gates before the masses strike the floor.
- Use scales to measure the total mass of the glider, string and weight stack. Record this value.
- Attach the full weight stack (6 x 10g masses) to the end of the string.
- Make sure the trolley is in position. Push the trolley.
- Remove one weight and attach it to the trolley using blu-tack. This will keep the total mass constant. (The weight stack is being accelerated too.)
- Repeat steps 6-7 removing one weight from the stack each time. Remember to attach each weight to the trolley as it is removed from the weight stack.
Results
Record the results in a suitable table, similar to the example results below:
Number of weights on stack Force in N Acceleration in m/s² - Run 1 Acceleration in m/s² - Run 2 Acceleration in m/s² - Run 3 Acceleration in m/s² - Mean 6 0.6 2.90 2.95 3.05 2.97 5 0.5 2.21 2.36 2.26 2.28 4 0.4 1.93 1.78 1.83 1.85 3 0.3 1.65 1.54 1.49 1.56 2 0.2 1.32 1.27 1.42 1.34 1 0.1 1.16 1.11 1.26 1.18 Analysis
- Plot a scatter graph with force on the vertical axis, and acceleration on the horizontal axis. Draw a suitable line of best fit.
- Describe what the results show about the effect of increasing the force which is accelerating the object.
- Extension: calculate the gradient of your graph and compare this to the to total mass of the glider and weight stack measured in step 4 above.
Evaluation
Acceleration is direcly proportional to the force applied to the object. This means that a graph of force against acceleration should produce a straight line that passes through the origin.
To what extent do your results show this relationship? For example, do all your points lie on a straight line passing through the origin, or are there any anomalous points?
-
-