Section outline
-
-
Do liquids exert pressure? What do you think? To find out the answer, watch the YouTube video below:
Revision Monkey. (2020). Pressure in liquids. (Standard YouTube licence)
-
Liquids will exert pressure on an object in the liquid as well as on the walls and base of the container in which it resides. Pressure in a liquid acts in all directions.
Activity
In the video you watched, the presenter explained the experiment on proving that the pressure is higher the deeper the liquid is. Now it's time for you to prove that yourself!
- Source an empty plastic bottle
- Fill it up with water
- Starting at the top of the bottle and working your way down, insert holes at regular intervals
- Note how the water travels out of the bottle
Water coming out of the hole at the lowest part of the bottle will travel further than water coming out of the top hole - this is due to the fact that there is a higher pressure in the liquid at the bottom of the bottle, as well as more weight on the liquid at the bottom.As the depth of the liquid increases, so too does the weight of the liquid and therefore the pressure increases with depth.
-
Let's look at this in a little more depth. Think of a liquid containing lots of water balloons on top of each other, as illustrated below.

The weight of a balloon on the top pushes downward force onto the balloons below. The balloons below need to counter this downward force by pushing a stronger upward force. The balloons at the bottom are required to support the weight of all the balloons above them and experience increased pressure. Should the water balloons be in a container, the balloons at the bottom will exert sideways force against the walls of the container, since they are being squashed by the weight of the balloons on top of them.
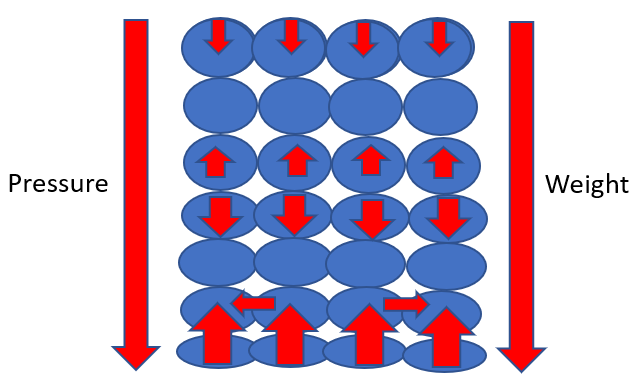
You should now clearly understand why, when you insert holes in a full water bottle, the water travels further through the bottom hole as opposed to the top hole. It's all down to pressure!

Imagine now how much pressure a submarine must endure when it deep dives. The amount of pressure and weight exerted on its structure is astronomical. Imagine too the effect of this increased pressure on the human body when a person deep dives, especially with no oxygen tank support.
-
How to calculate pressure in a liquid
The formula to calculate pressure in a liquid is:
\[P=hg\rho \]
...but how did we get to this? Review the steps below to find out:- P = F ÷ A
- We know that force = mass x gravitational pull i.e.
- \[F=mg\]
- Mass = volume x density i.e.
- \[M=lwh\rho \]
- therefore:
- \[F=lwhg\rho \]
- We know that A = length x width therefore
- \(P=lwhg\rho \div \)lw
- Cancel out the two sets of lw and you get the result:
- \[P=hg\rho \]
To put this in words:
Pressure in liquids = height of the liquid column x density of liquid x acceleration due to gravity.
It's important to understand that pressure in a liquid isn't dependent on the area or shape of the container, but rather on the depth and density of the liquid.
- P = F ÷ A
-
Watch the YouTube video below (start at 4:30) in which the presenter thoroughly explains how to calculate the pressure in a liquid.
The Organic Chemistry Tutor. (2018). Introduction to pressure and fluids (Standard YouTube licence)
-
Let's summarise the characteristics of pressure in liquids:
- The greater the depth the greater the pressure
- Pressure in a liquid acts in all directions
- The higher the density of a liquid the higher the pressure
A further interesting example of pressure in liquids is the following: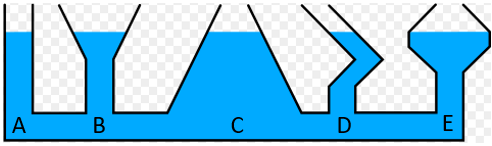
When water, or any liquid, is poured into a communicating vessel like the one above, the liquid will be at the same level in all the tubes, irrespective of their shape. This is due to the fact that the pressure is the same at all points of similar depths. The pressure at A = the pressure at B = C = D = E.
-
Pressure in liquids and upthrust
Going back to our illustration of water balloons, but this concept will be relevant for any object placed in a liquid:
You now know that the liquid at the bottom will experience greater pressure than the liquid at the top. The difference in this pressure will result in an upward force known as an upthrust.
The horizontal forces increase with depth but these horizontal forces balance each other out with zero net effect.
-
Example 1
Let's look at this concept by way of an example:
A cube sized 2 cm on each side is submerged in water. The bottom of the cube is at a depth of 10 cm. Assume the following:
- Ρ (the density of water) = 1027 kg/m3
- g = 10 N/kg
- Remember the formula for pressure = hΡg
What is the difference in the pressure between the top and bottom of the cube?Pressure at the bottom
Pressure = hΡg
= 0.1 m x 1027 kg/m3 x 10 m/s2
= 1027 N/m2Pressure at the top
The depth at the top = 0.1 m - 0.02 m (since the sides are 2 cm)
= 0.08 m x 1027 kg/m3 x 10 m/s2
= 821.6 N/m2
The difference in pressure between the bottom and top:
= 1027 N/m2 - 821.6 N/m2
= 205.4 N/m2 - Ρ (the density of water) = 1027 kg/m3
-
Example 2
Using the same assumptions and cube size detailed above, let's work out what the difference in force will be between the top and bottom of the cube.
Pressure = Force ÷ Area
=> Difference in pressure = Difference in force ÷ Area
=> Difference in force = Difference in pressure x Area
Area of a cube = length2
= (0.02 m)2
= 0.0004 m2Difference in force = Difference in pressure x Area
= 205.4 N/m2 x 0.0004 m2
= 0.0822 N
The above number therefore represents the upthrust of force. -
Watch the YouTube video below which clearly explains pressure in liquids and upthrust. This video will also help you understand why some objects float and others sink in a liquid.
GCSE Physics. Cognito. (2020). Liquid pressure and upthrust (Standard YouTube licence)
-
Pascal's Principle
Pascal's principle of pressure transmission in fluids states that a pressure change at any point in a confined incompressible fluid is transmitted throughout the fluid such that the same change occurs everywhere. (Wikipedia)
Put differently: if a pressure is applied to a liquid in a closed contained space, the pressure is transmitted equally in all directions to all parts of the liquid and container walls.
Watch the short YouTube video below which illustrates Pascal's principle:
myhometuition. (2017). Pascal's Principle (Standard YouTube licence)
-
The image below illustrates Pascal's Principle:
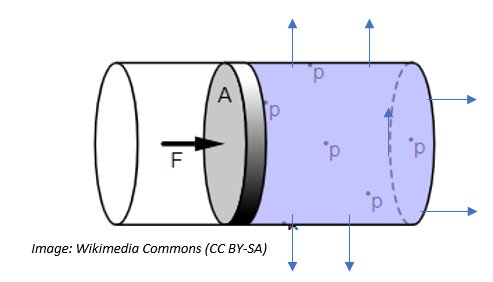
Remember that if holes are inserted into this container, the liquid will be dispersed the same distance, no matter the direction. The more pressure that is applied to the liquid in the contained space, the further the liquid will travel.
Examples of where Pascal's principle is applied include hydraulic car jacks, car brakes and many mechanical bulldozers.
If you're interested, watch the YouTube video below which illustrates how hydraulic brakes function in a vehicle.
Simon. (2020). How do hydraulic brakes in cars and light vehicles work. (Standard YouTube licence)
-
