Sectieoverzicht
-
So far, we have had lots of practice calculating the values of different trig ratios. But why bother? What is the purpose of it all?
Trigonometry allows us to solve all sorts of problems in the real world. For example, a lighthouse is \( 80 \text{ m} \) tall. A ship out at sea measures the angle to the top of the lighthouse as \( 13.78^\circ \). How far away is the ship from the lighthouse?
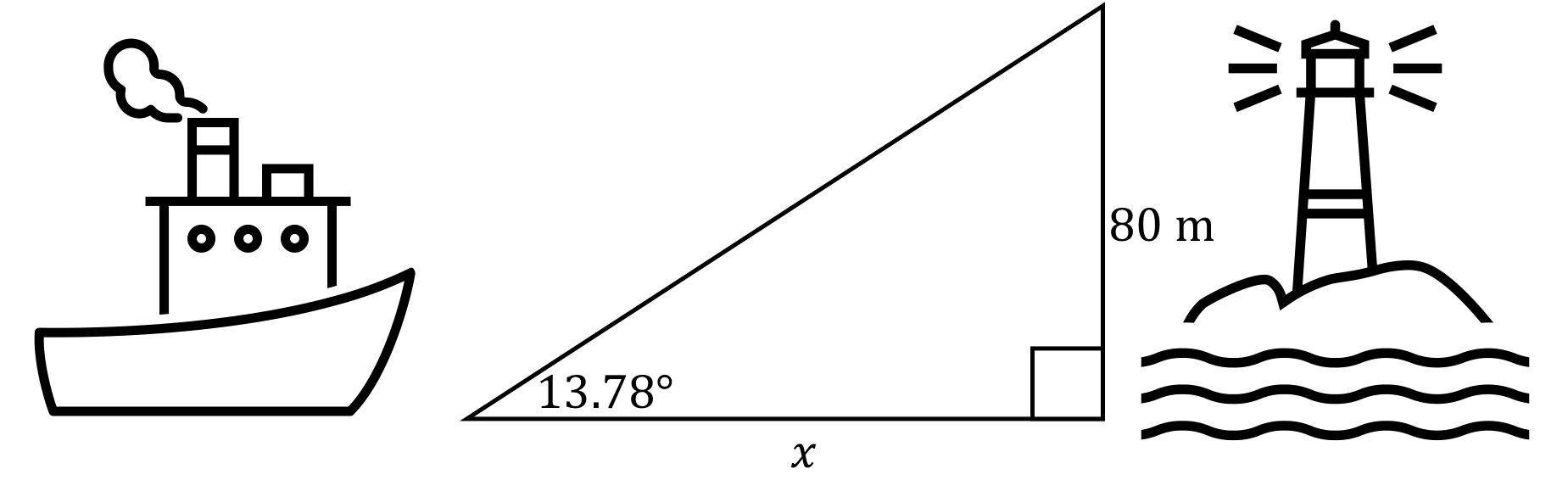
Before we can solve this problem, there are a few things we need to know.
Firstly, an angle of elevation is an angle measured UP from the horizontal. In the situation above \( 13.78^\circ \) is the angle of elevation.
Secondly, an angle of depression is the angle measured DOWN from the horizontal.
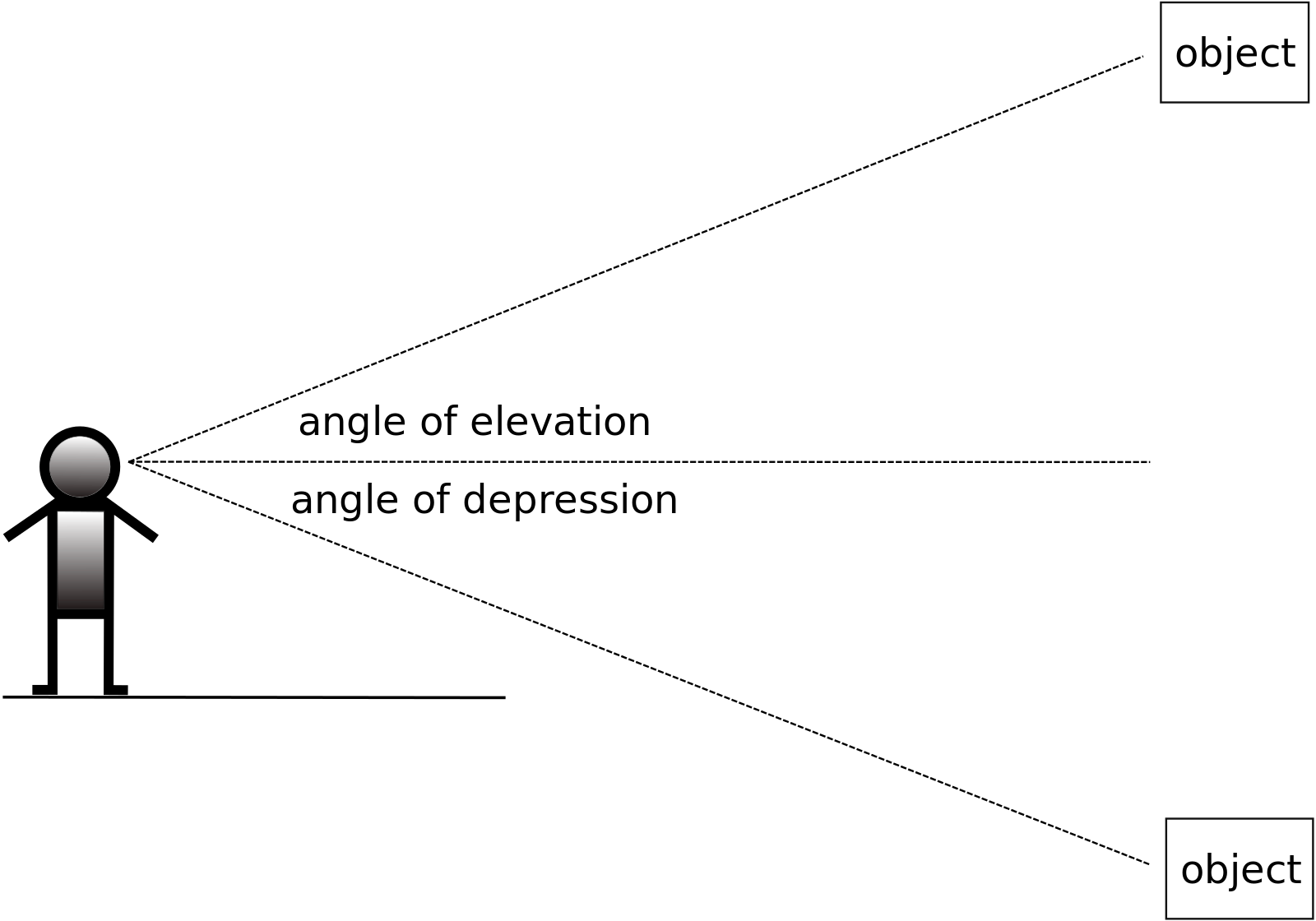
Finally, we also need to know how to use our trig ratios to find the lengths of unknown sides.
-
Activity 1: Finding the lengths of unknown sides
It’s time to start using trigonometry to solve real problems. One of the most commons types of problems you will encounter is to find the length of an unknown side in a right-angled triangle.
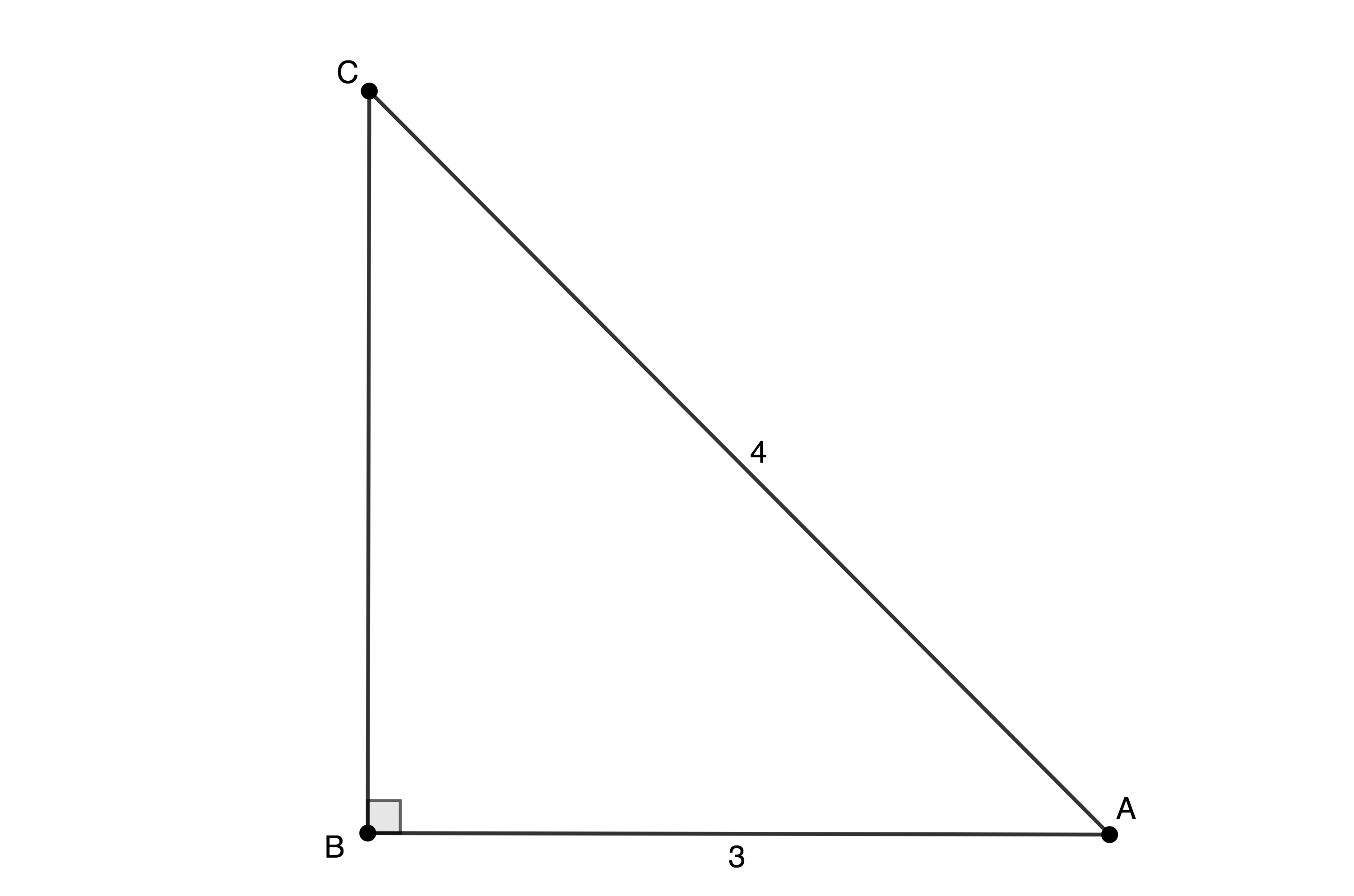
Have a look at the triangle below. Because it is a right-angled triangle and because we know the length of two sides, we can easily find the length of the third side by using Pythagoras’ Theorem.
Now look at the next triangle below. In this case, we only know the length of one of the sides so we cannot use Pythagoras. But we do have another piece of information. We know the size of one of the non-right angles.
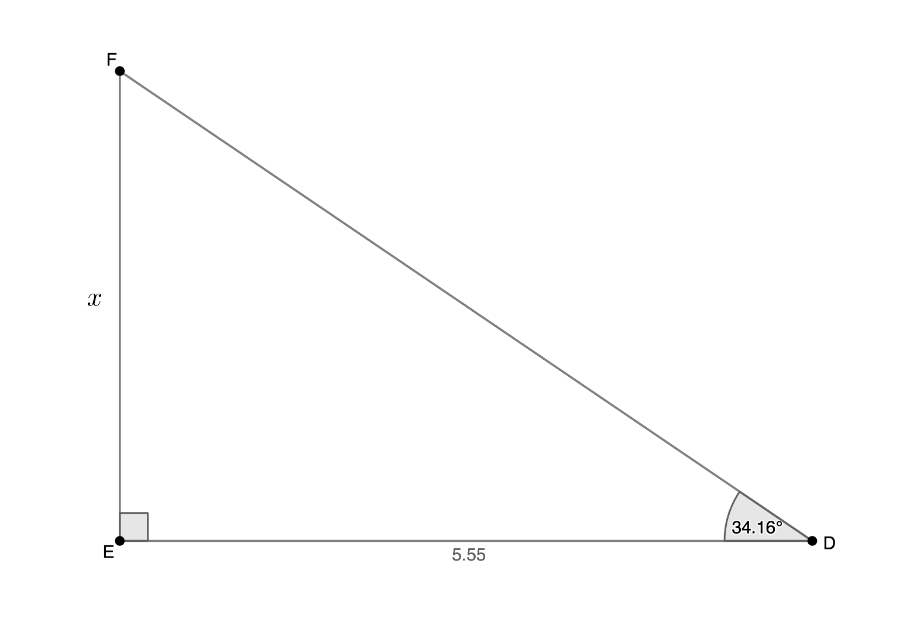
With respect to the known angle, which trig ratio combines the length of the side we know (\( DE \)) and the length of \( x \), the side we are trying to find (\( EF \))?
With respect to \( \hat{\text{D}} \), we know the length of the adjacent side, and we want to find the length of the opposite side. Therefore, we can use tangent and say that \( \tan 34.16^\circ =\displaystyle \frac{\text{opp}}{\text{adj}}=\displaystyle \frac{EF}{DE}=\displaystyle \frac{x}{5.55} \). In other words, \( \tan 34.16^\circ =\displaystyle \frac{x}{5.55} \).
Now we have an equation that we can solve.
\( \begin{align*}\tan 34.16^\circ & =\displaystyle \frac{x}{5.55}\\\therefore x & =\tan 34.16^\circ \times 5.55\end{align*} \)
But what is the value of \( \tan 34.16^\circ \)? We can use any scientific calculator to find the value of any of the trig ratios for any angle. See the sequence of key presses required for different calculators. You will need to check which sequence your calculator uses.
Casio calculators (direct input): \( \boxed{\tan}\to \boxed{34.16}\to\boxed{)}\to\boxed{=} \)
Other calculators (indirect input):\( \boxed{34.16}\to\boxed{\tan}\to\boxed{=} \)
In either case, you should get that \( \tan 34.16^\circ =0.678579...\approx 0.679 \). Note that in this unit we will mostly show the Casio calculator key sequence.
Note In most situations the answers you get from your calculator for the value of a trig ratio are non-terminating, non-repeating decimals. For the greatest accuracy, round off only your final answerand round off to three decimal places unless told otherwise. Now we can solve for $latex \scriptsize x$ in our original equation.
\( \begin{align*}\tan 34.16{}^\circ & =\displaystyle \frac{x}{{5.55}}\\\therefore x & =\tan 34.16{}^\circ \times 5.55\\&=3.766\end{align*} \)
\( \boxed{\tan}\to \boxed{34.16}\to\boxed{)}\to\boxed{\times}\to\boxed{5.55}\to\boxed{=}\)
-
Activity 2: Example 1
Use your calculator to calculate the following correct to three decimal places:
- \( \cos 58^\circ \)
- \( 2\times \sin 13.56^\circ \)
- \( \displaystyle \frac{{\cos 67.3^\circ }}{{\sin 41.97^\circ }}\)
Solution
- \( \boxed{\cos}\to\boxed{58}\to\boxed{)}\to\boxed{=}\to 0.530 \)
- \( \boxed{2}\to\boxed{\times}\to\boxed{\sin}\to\boxed{13.56}\to\boxed{)}\to\boxed{=}\to0.469 \)
- \( \boxed{\cos}\to\boxed{67.3}\to\boxed{)}\to\boxed{\div}\to\boxed{\sin}\to\boxed{41.97}\to\boxed{)}\to\boxed{=}\to0.577 \)
Note When calculating the value of trig ratios, make sure that your calculator is in DEGREE mode. You should see a small D or DEG symbol on screen. If you do not, consult your calculator’s manual for how to change back to DEGREE mode. -
Activity 3: Example 2
Find the length of (correct to three decimal places).
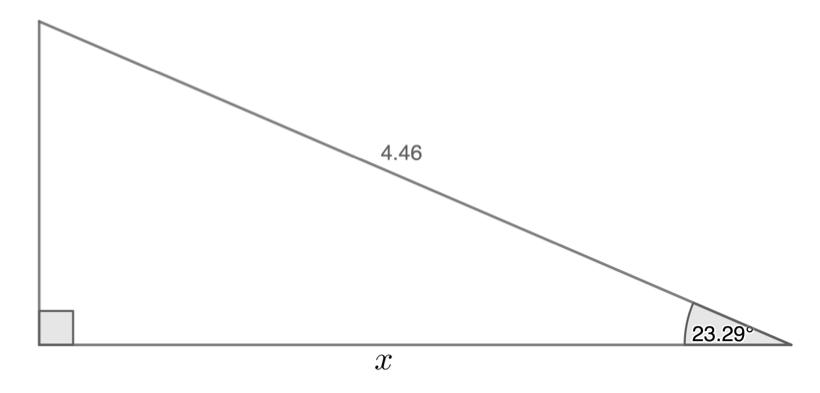
Solution
With respect to the angle that we have, we know the hypotenuse and we want the adjacent side. Cosine is the ratio that combines adjacent and hypotenuse.
\( \begin{align*}\cos 23.29{}^\circ & =\displaystyle \frac{x}{{4.46}}\\\therefore x & =4.46\times \cos 23.29{}^\circ \\ & =4.097\end{align*} \)
\( \boxed{4.46}\to\boxed{\times}\to\boxed{\cos}\to\boxed{23.29}\to\boxed{)}\to\boxed{=}\to4.097 \)If you would like to see some additional simple worked examples watch these two videos:
- SOHCAHTOA - Finding Missing Sides PART 1 (Duration: 04.37)
- SOHCAHTOA - Finding Missing Sides PART 2 (Duration: 02.34)
- SOHCAHTOA - Finding Missing Sides PART 1 (Duration: 04.37)
-
Activity 4: Problems involving angles of elevation
Now we can return to our original lighthouse problem. Here it is again.
A lighthouse is \( 80 \text{ m} \)tall. A ship out at sea measures the angle to the top of the lighthouse a\( 13.78^\circ \). How far away is the ship from the lighthouse?
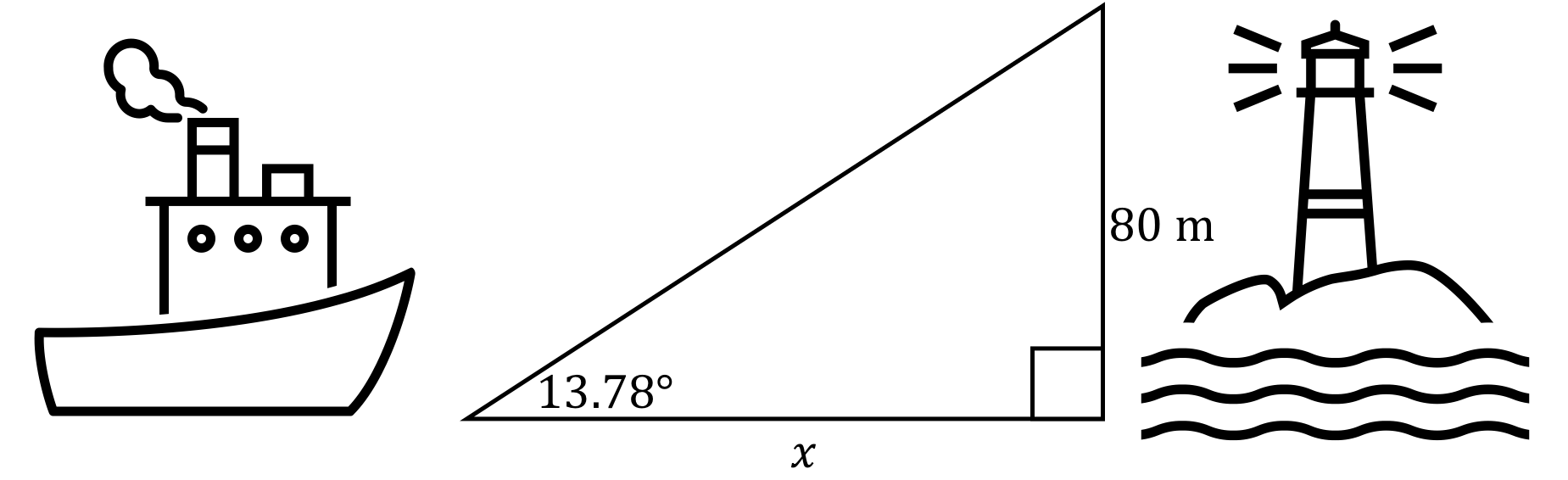
Solution
If you are not given a sketch of the situation, draw your own.
Relative to the angle that we have, we know the opposite side and we want the adjacent side. Tangent is the ratio that combines opposite and adjacent.
\( \begin{align*}\tan 13.78^\circ & =\displaystyle \frac{80}{x} \\\therefore x & =\displaystyle \frac{80}{\tan 13.78^\circ } \\ & =326.193\ \text{m}\end{align*}\)
Don’t forget to include the units (metres) in your final answer.
-
Activity 5: Problems involving angles of depression
Here is a problem that involves an angle of depression.
An stuntman planning to ramp a motorcycle between two buildings stands at the top of one of the buildings that he knows is \( 35\ \text{m} \) height and measures an angle of depression to the foot of the other building of \( 53.24^\circ \). How far apart are the buildings?
Solution
Remember that if no sketch is given of the situation, make your own. Do this now on a piece of paper and then compare it to the one below.

We can then draw an even simpler diagram like this.

Notice how the angle of depression is \( 53.24^\circ \). Therefore, the angle inside the triangle is \( 36.76^\circ \) because these two angles add up to \( 90^\circ \). We can now solve for \( x \), the distance between the buildings.
Relative to the angle that we have, we know the adjacent side and we want the opposite side. Tangent is the ratio that combines opposite and adjacent.
\( \begin{align*}\tan 36.76^\circ & =\displaystyle \frac{x}{35} \\\therefore x & =35 \times \tan 36.76^\circ \\ & =26.15\ \text{m}\end{align*}\)
Don’t forget to include the units (metres) in your final answer.
-
Activity 6: Additional online angle of elevation and depression examples and practice
- Angles of Elevation and Angle of Depression - Definition and Examples: Read more on angles of elevation and depression and get more practice working through example problems.
- Angles of elevation and depression: Work through additional angles of elevation and depression examples.
- Fly-by calibration: Play with a unique interactive simulation to get more practice using trig and angles of depression to solve real problems.
- Angles of Elevation and Angle of Depression - Definition and Examples: Read more on angles of elevation and depression and get more practice working through example problems.
-
