Sectieoverzicht

  • Almost always, you will have to work with triangles where the angles are not \( 30^\circ \), \( 45^\circ \), or \( 60^\circ \). In these cases, you will need a scientific calculator to help you. However, when the triangle you are working with does contain \( 30^\circ \), \( 45^\circ \), or \( 60^\circ \), you should recognise these as the special angles and remember what the corresponding trigonometric ratios are.
    • Leerlingen moeten
      Als voltooid aanduiden

      Activity 1: Using a calculator

      Question: Use a calculator to work out what \( \tan 34.16^\circ \) is.

      Answer:
      If your calculator is direct input (e.g. most Casio calculators) key in the question like this:
      \( \boxed{\tan}\to \boxed{34.16}\to\boxed{)}\to\boxed{=} \)

      If you calculator is not direct input (e.g. most Sharp calculators_ key in the question like this:
      \( \boxed{34.16}\to\boxed{\tan}\to\boxed{=} \)

      In either case, your calculator should give you that \( \tan 34.16{}^\circ =0.678579...\approx 0.679 \).
    • Leerlingen moeten
      Als voltooid aanduiden

      Activity 2: The special angles

      Question: Have a look at the three right-angled triangles below.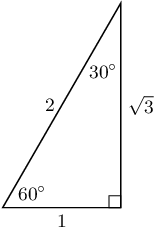

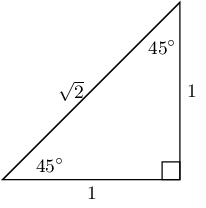
      30 degrees45 degrees
      Now draw a table like this and work out the various trig ratios to complete it.

      \( 30^\circ \) \( 45^\circ \) \( 60^\circ \)
      \( \sin \)
      \( \cos \)
      \( \tan \)


      Answer: You should find that your table looks like this

      \( 30^\circ \) \( 45^\circ \) \( 60^\circ \)
      \( \sin \)
      		\( \displaystyle\frac{1}{2} \) \( \displaystyle\frac{1}{\sqrt{2}} \) \( \displaystyle\frac{\sqrt{3}}{2} \)
      \( \cos \)
      		\( \displaystyle\frac{\sqrt{3}}{2} \) \( \displaystyle\frac{1}{\sqrt{2}} \) \( \displaystyle\frac{1}{2} \)
      \( \tan \)
      		\( \displaystyle\frac{1}{\sqrt{3}} \) \( \displaystyle\frac{1}{1} \) \( \displaystyle\frac{\sqrt{3}}{1} \)

      \( 30^\circ \), \( 45^\circ \) and \( 60^\circ \) are called special angles because we don't need to use a calculator to work them out. They give ratios that are easy to right down as fractions and these fractions express their value exactly.

      Remember when we calculated the value of \( \tan 34.16^\circ \) above? The calculator gave us the answer \( =0.678579... \). The calculator had to round the answer off. We then rounded the answer off further to \( \approx 0.679 \). Therefore, the answer was not exact.

      The three special angles above allow us to express the trig ratios as simple fractions that represent the exact answer.

      This means that when we have these special angles, we can work without a calculator.
    • Leerlingen moeten
      Als voltooid aanduiden

      Activity 3: Example 1

      Determine the value of the following WITHOUT a calculator:

      1. \( \sin 30^\circ \)
      2. \( \tan 45^\circ \)
      3. \( \cos 60^\circ \)
      4. \( \sin^2 60^\circ + \cos^2 60^\circ \)

      Solution

      When asked to determine the value of trig ratios without a calculator, you know you have to use the three special angles. It can help to make quick small sketches of the triangles with these angle in on the side of your page, like this.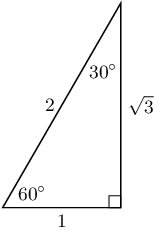
      3045

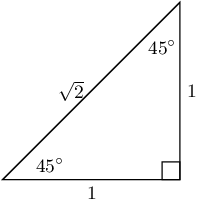
      1. \( \sin 30^\circ = \displaystyle\frac{1}{2} \)
      2. \( \tan 45^\circ =1 \)
      3. \( \cos 60^\circ = \displaystyle\frac{1}{2}\)
      4. \( \sin^2 60^\circ + \cos^2 60^\circ =\displaystyle \left(\frac{\sqrt{3}}{2} \right)^2 + \displaystyle \left(\frac{1}{2} \right)^2 = \displaystyle\frac{3}{4}+\displaystyle\frac{1}{4}=1 \)

    • Special angles Test
      Leerlingen moeten
      Als voltooid aanduiden