Sectieoverzicht

  • To lay the foundation for understanding what trigonometry is and how it works, do this next activity.


    • Leerlingen moeten
      Als voltooid aanduiden

      Activity 1: Investigate the sides of similar triangles

      Time required: 20 minutes

      What you need:

      • a pen or pencil
      • paper
      • a protractor
      • a ruler

      What to do:

      1. Draw three triangles of different sizes using a protractor and a ruler so that each triangle has interior angles equal to \( 30^ \circ \),0\( 60^ \circ \) and \( 90^ \circ \) as shown below. We call these ‘similar triangles’ because they are all the same shape, but not the same size. 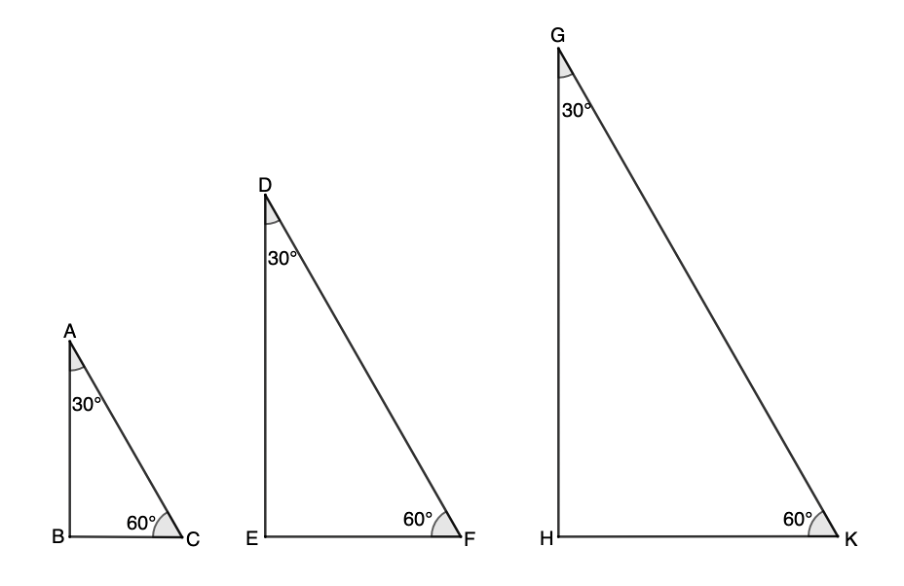If you do not have a protractor or ruler, you can measure the lengths of the triangles below instead of your own.Activity 1 
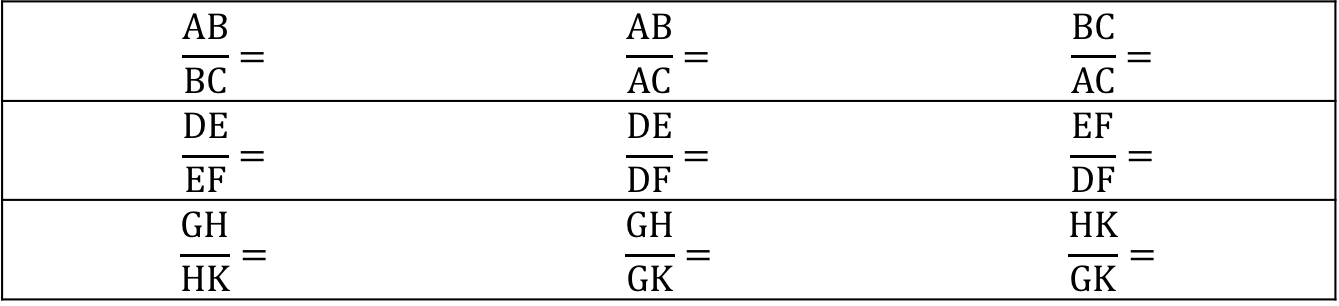
      2. Now measure the angles and lengths accurately and complete the following table. Leave all your ratios as fractions for now.
        table
      3. What do you notice about each of the ratios? You can convert each ratio to a decimal if this helps you to compare. Does it matter what the lengths of the sides of the triangles are if the angles inside the three triangles stay the same size?
      4. Draw one more right-angled triangle but this time make the other two angles \( 40^ \circ \) and \( 50^ \circ \). Measure the lengths of the sides as before. Are the sides in the same ratio as the first three triangles that you drew?

      What did you find?

      You should have found that the value of each of the ratios of corresponding sides in each triangle was always the same. In other words, \( \displaystyle \frac{{\text{AB}}}{{\text{BC}}}=\displaystyle \frac{{\text{DE}}}{{\text{EF}}}=\displaystyle \frac{{\text{GH}}}{{\text{HK}}}\), \( \displaystyle \frac{{\text{AB}}}{{\text{AC}}}=\displaystyle \frac{{\text{DE}}}{{\text{DF}}}=\displaystyle \frac{{\text{GH}}}{{\text{GK}}}\) and \( \displaystyle \frac{{\text{BC}}}{{\text{AC}}}=\displaystyle \frac{{\text{EF}}}{{\text{DF}}}=\displaystyle \frac{{\text{HK}}}{{\text{GK}}}\).

      This means that it is the size of the angles in a triangle that determines the ratios between the lengths of the sides. It does not matter how big or small the triangle is. If the sizes of the angles stay the same, the corresponding sides will always be in the same ratio. If we change the sizes of the angles, we change the ratio of the sides.

    • Leerlingen moeten
      Als voltooid aanduiden

      Activity 2: Optional internet activity

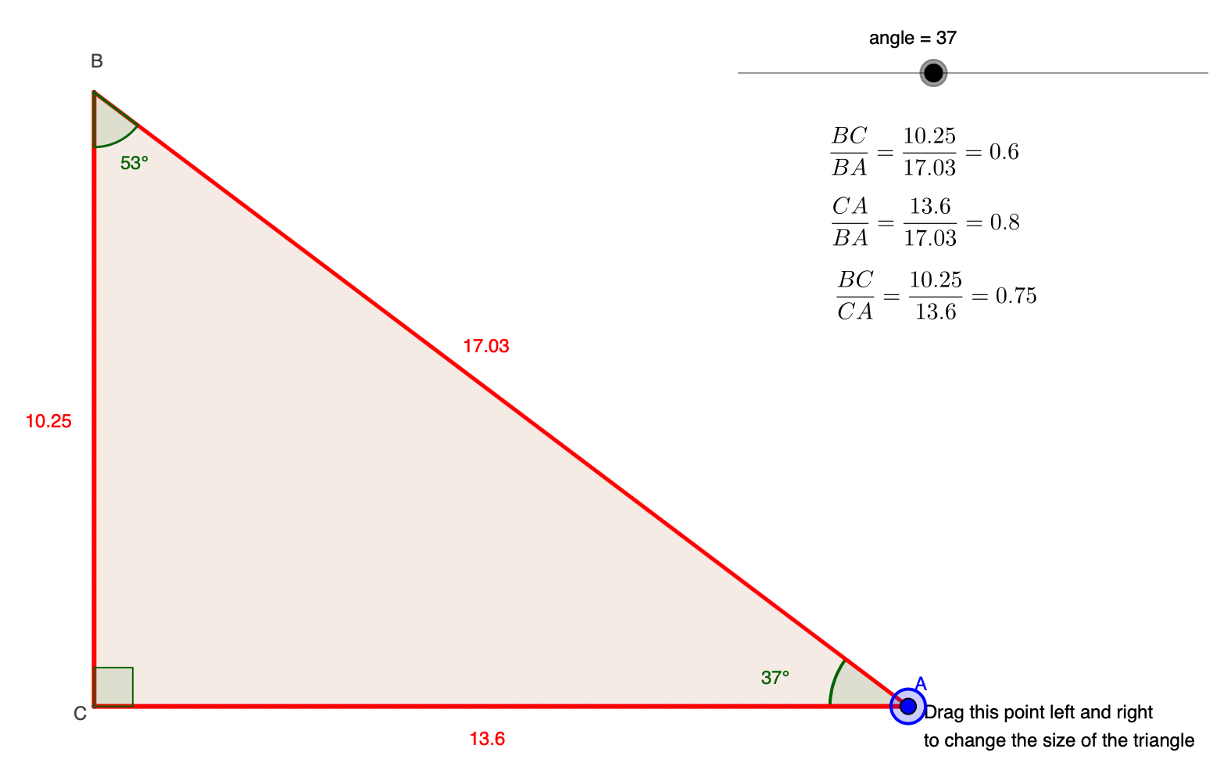
      If you have an internet connection, continue to explore how it is the angles inside a right-angled triangle that determine the ratio of the sides of the triangle by playing with the Right Triangle Ratios interactive tool. Drag the slider to change the angle. See how the ratios of the sides change? Drag point A left and right to change the size of the triangle with a given angle. See how the ratio of the sides stays the same?

      Right Triangle Ratios

      What ratios do you get when you make the angle \( 30^ \circ \) or \( 60^ \circ \).