The Theorem of Pythagoras

Before you start this course, you need to make sure that you know and can use the Theorem of Pythagoras to find the length of unknowns sides in right angled triangles.

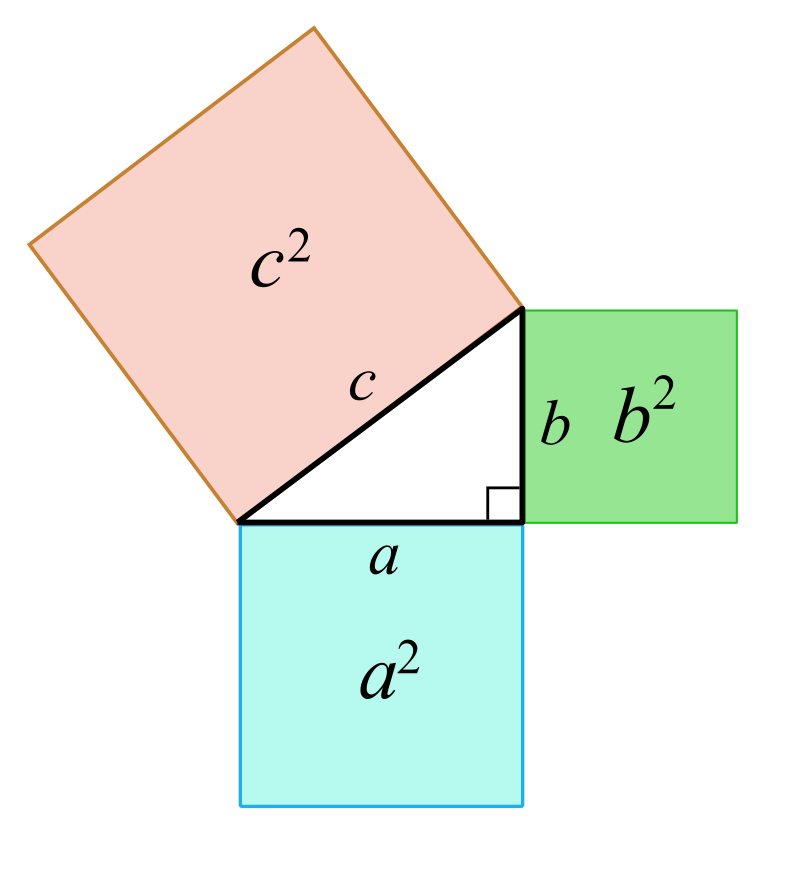
The Theorem of Pythagoras states that for any right-angled triangle the square of the length of the hypotenuse (always the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. In other words, in the triangle below, it means that \( c^2=a^2+b^2 \).

Try answering the following question to make sure you understand the theorem and how to use it.

In \( \Delta ABC \), \( \hat {A}=90 ^\circ \), \(\text{AB}=4.5\,\text{cm}\) and  \(\text{BC}=7\,\text{cm}\). Calculate the length of \(\text{AC}\).

Solution:

\( \Delta \text{ABC}\) is a right-angled triangle. Therefore, we can use the Theorem of Pythagoras to calculate the length of the \( \text{AC}\).

\( \begin{align}\text{B}{{\text{C}}^{2}}&=\text{A}{{\text{B}}^{2}}+\text{A}{{\text{C}}^{2}}\\\therefore \text{A}{{\text{C}}^{2}} &=\text{B}{{\text{C}}^{2}}-\text{A}{{\text{B}}^{2}}\\\therefore \text{AC}&=\sqrt{{\text{B}{{\text{C}}^{2}}-\text{A}{{\text{B}}^{2}}}}\\ &=\sqrt{{{{7}^{2}}-{{{4.5}}^{2}}}}\\ &=\sqrt{{49-20.25}}\\&=\sqrt{{28.75}}\\&=5.36\end{align} \)