Sectieoverzicht
-
-
Leerlingen moetenAls voltooid aanduiden
The circle
Circles are very special shapes. They have no straight edges. Instead they are defined by every point on the circle being exactly the same distance from a single point, the centre. This distance is called the radius (r).
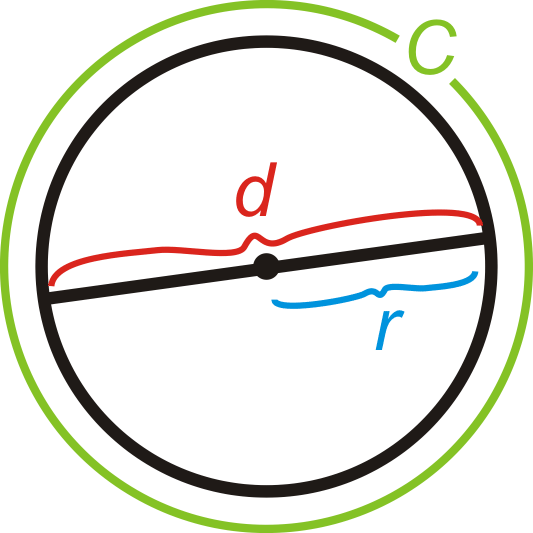
The diameter (d) of a circle is the straight line that passes from one side of the circle to the other through the centre. Therefore it is twice the length of the radius.
Because circles are so special, we give their perimeter a special name - the circumference (C).
-
Leerlingen moetenAls voltooid aanduiden
What is Pi?
Before we learn about how to find the circumference and area of circles, we need to know one more thing that makes circles so special.
If you measure the diameter and circumference of any circle, it turns out that the ratio of the length of the circumference to the length of the diameter is always the same value, about 3.14. This is a very special number which we call\( \pi \) /(pi).
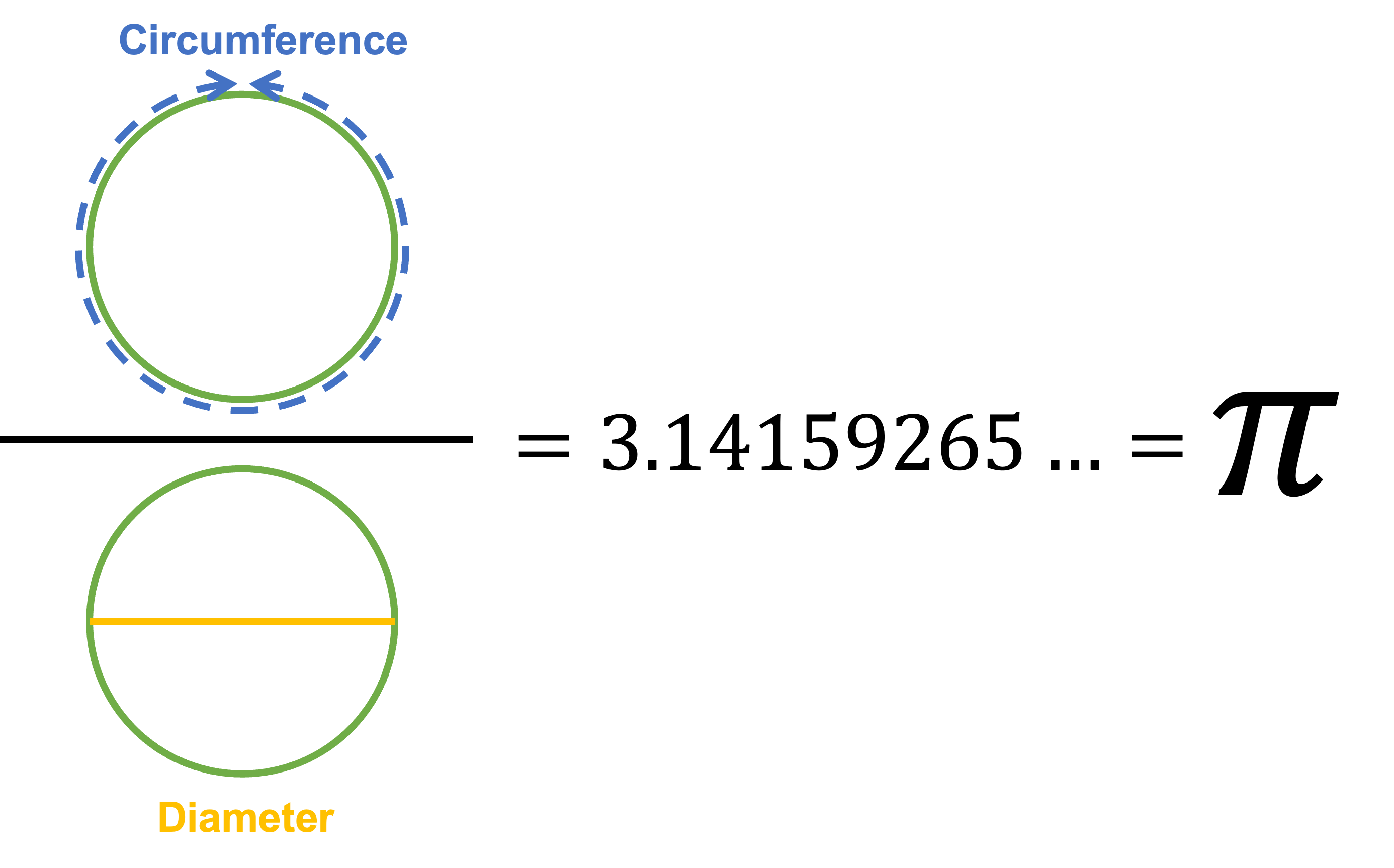
Watch this Animation of Pi (with narration) (1:11) for an excellent visual explanation.
-
Leerlingen moetenAls voltooid aanduiden
Activity: Interactive challange
Work through this interactive challenge from CK-12 to practice working with \( \pi \) and the diameter and radius of a circle.
-
Leerlingen moetenAls voltooid aanduiden
Activity: Circumference of a circle
To learn how to find the circumference of a circle by working through this CK-12 FlexBook chapter called Circumference.
-
Leerlingen moetenAls voltooid aanduiden
Activity: Area of a circle
To learn how to find the area of a circle work through the CK-12 FlexBook chapter called Area of a Circle.
Now watch this example of finding the area of a circle.
-
Leerlingen moetenAls voltooid aanduiden
Activity: Interactive challenge
Work through this interactive challenge from CK-12 to practice finding the area of circles.
-
Leerlingen moetenAls voltooid aanduiden
-