Sectieoverzicht

    • Leerlingen moeten
      Als voltooid aanduiden

      Area of triangles


      We already know how to find the perimeter of any triangle. We add the lengths of the three sides. But how can we easily find the area of a triangle?

      1. Look at the shape below. ABCD is a parallelogram. What is the area of ABCD?

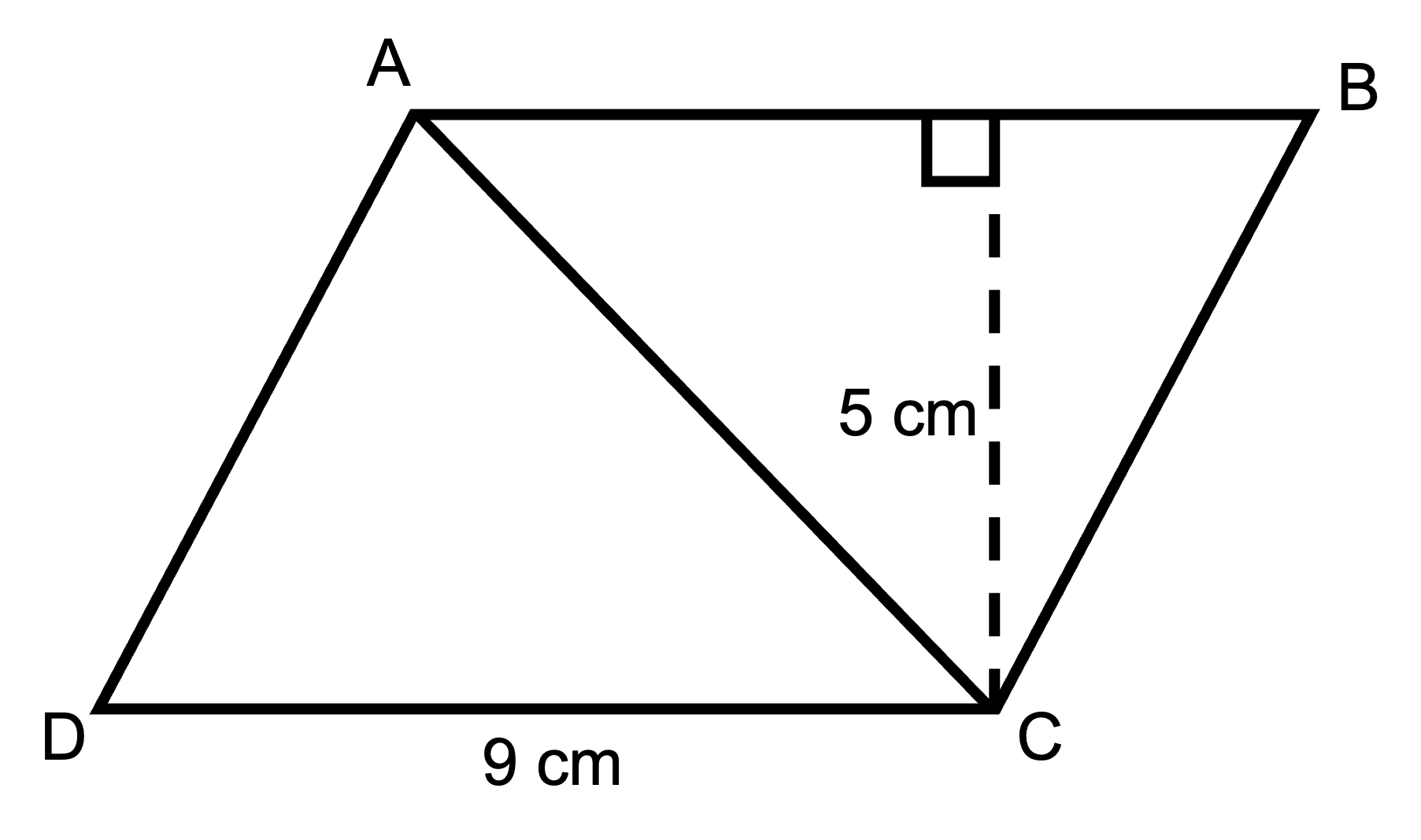
      areatri1

      2. What shape is ABC? What is the area of ABC? How do you know?

      3. What can you say about how to find the area of any triangle?

      Answer:

      The area of parallelogram ABCD is A = b x h = 9 cm x 5 cm = 45 cm2.

      ABC is a triangle. Its area is exactly half the area of the parallelogram. We have cut the parallelogram in half to create triangle ABC. Therefore, the area ABC is 22.5 cm2.

      We can always cut a parallelogram into two identical triangles. We can also arrange two identical triangles into the shape of a parallelogram. This means that the area of a triangle is always half the area of the parallelogram we could make from two of these triangles.

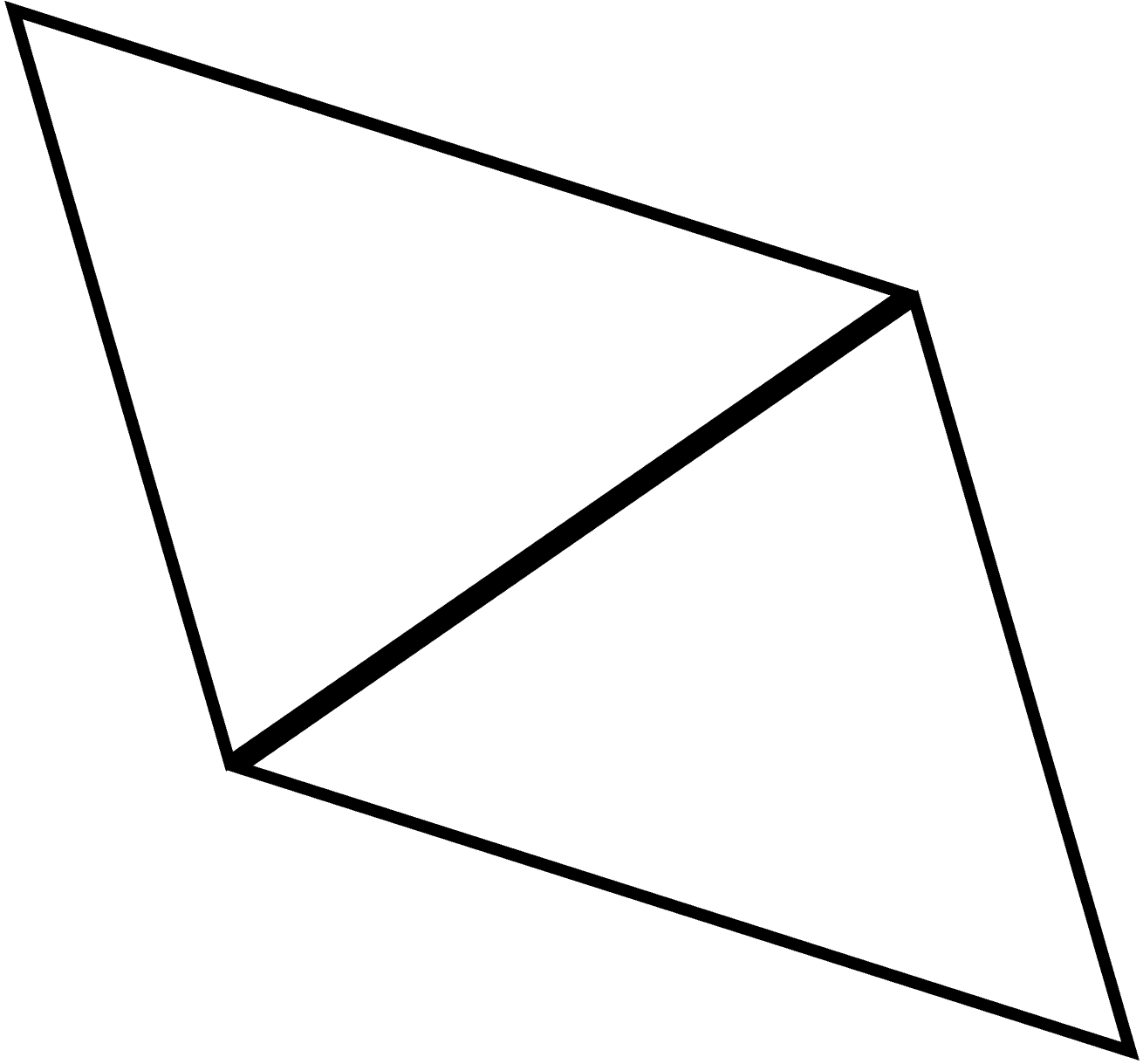
      areatri2

      In other words, the area of a triangle is \( \text{area of triangle} = \frac{1}{2}\text{area of parallelogram} \)

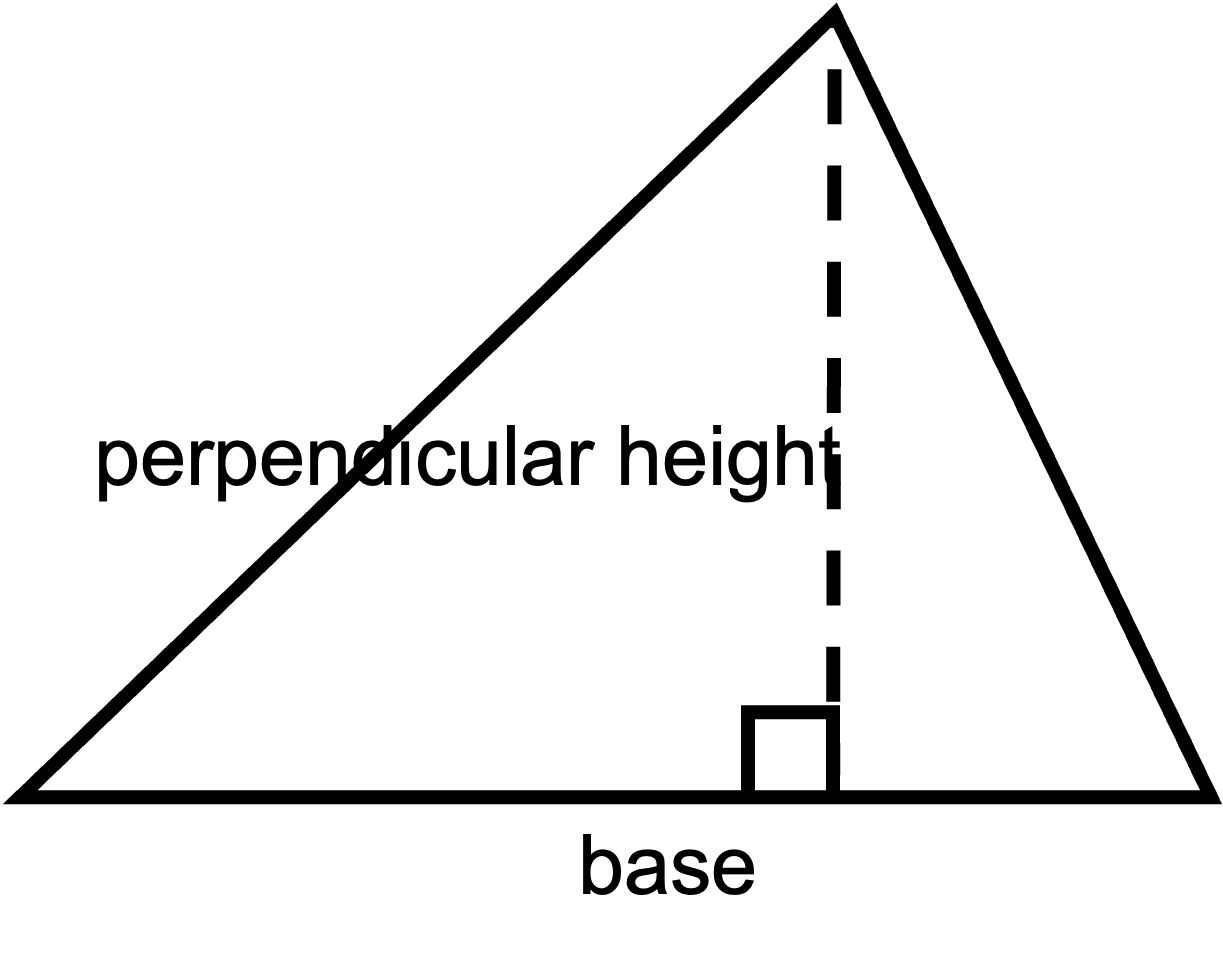
      \( A=\frac{1}{2}\left(\text{base}\times \text{perpendicular height}\right) \)

      \( A=\frac{1}{2}bh \)

      areatri3

      Learn more by working through the CK-12 FlexBook chapter called Area of Triangles.

    • Find the area of triangles (TBC) Test
      Leerlingen moeten
      Als voltooid aanduiden

      https://flexbooks.ck12.org/cbook/ck-12-middle-school-math-concepts-grade-8/section/8.1/related/lesson/area-and-perimeter-of-triangles-geom/