Section outline
-
-
Perimeter of parallelograms and trapezoids
We have learnt how to find the perimeter and area of rectangles (and squares). We can use this knowledge to help us easily find the perimeter and area of parallelograms and trapezoids.
Think about these 2 shapes. One is a rectangle and the other is a parallelogram that has been created by pushing the rectangle over a bit.
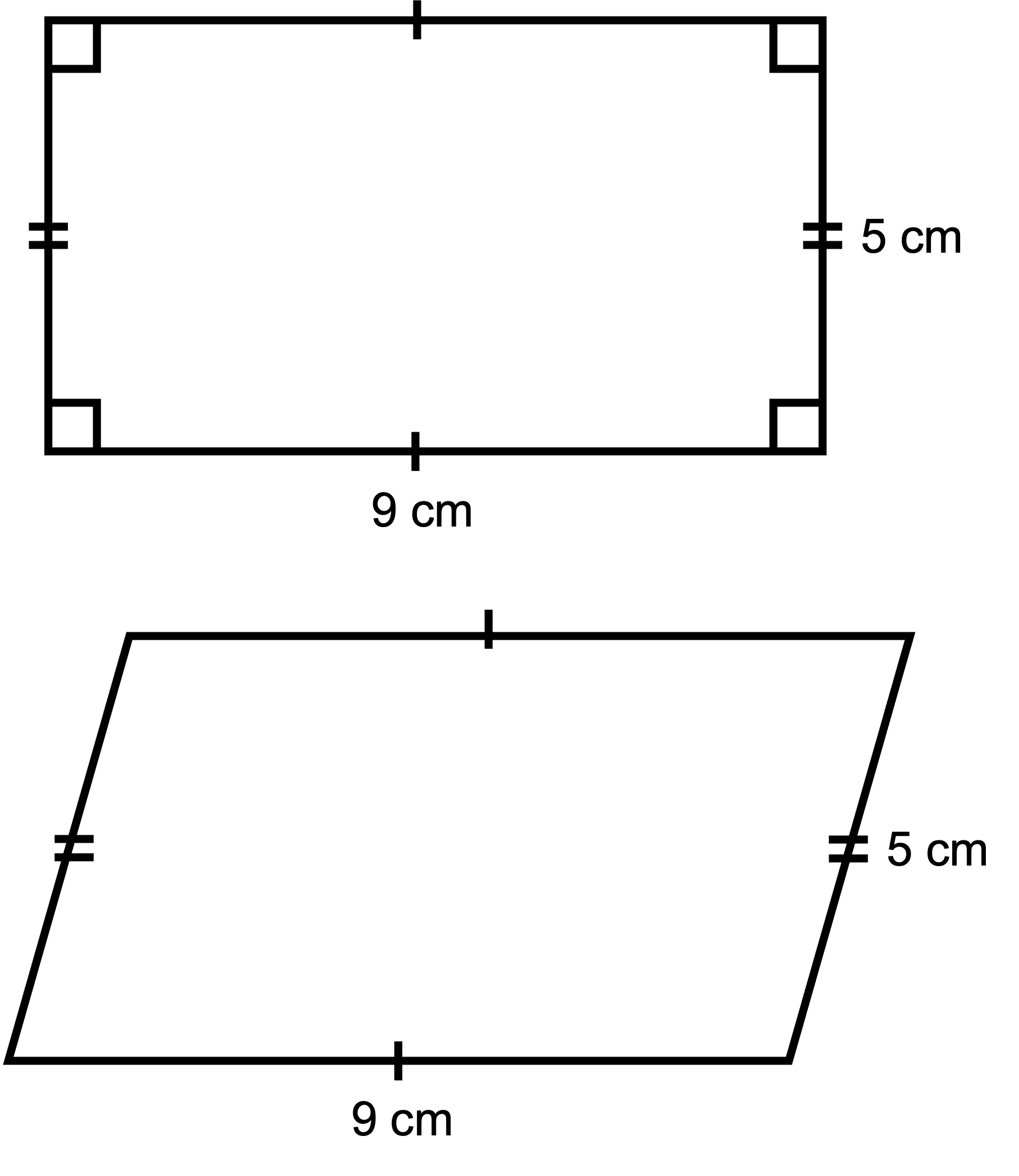
Question: Are the lengths of the sides of the parallelogram still the same? Has the perimeter of the shape changed?
Answer: The lengths of the sides have not changed and the length of the opposite sides of a parallelogram are always equal. Therefore, the perimeter of a parallelogram can be found the same way as the perimeter of a rectangle.
P = 2b + 2h (base and height) or P = 2l + 2b (length and breadth).
But what about a trapezoid? Remember, a trapeziod has only one pair of opposite sides parallel. Because the other two sides are not parallel, they can be different lengths.

If the non-parallel sides happen to be the same length then the shape is a special kind of trapezoid called a trapezium.
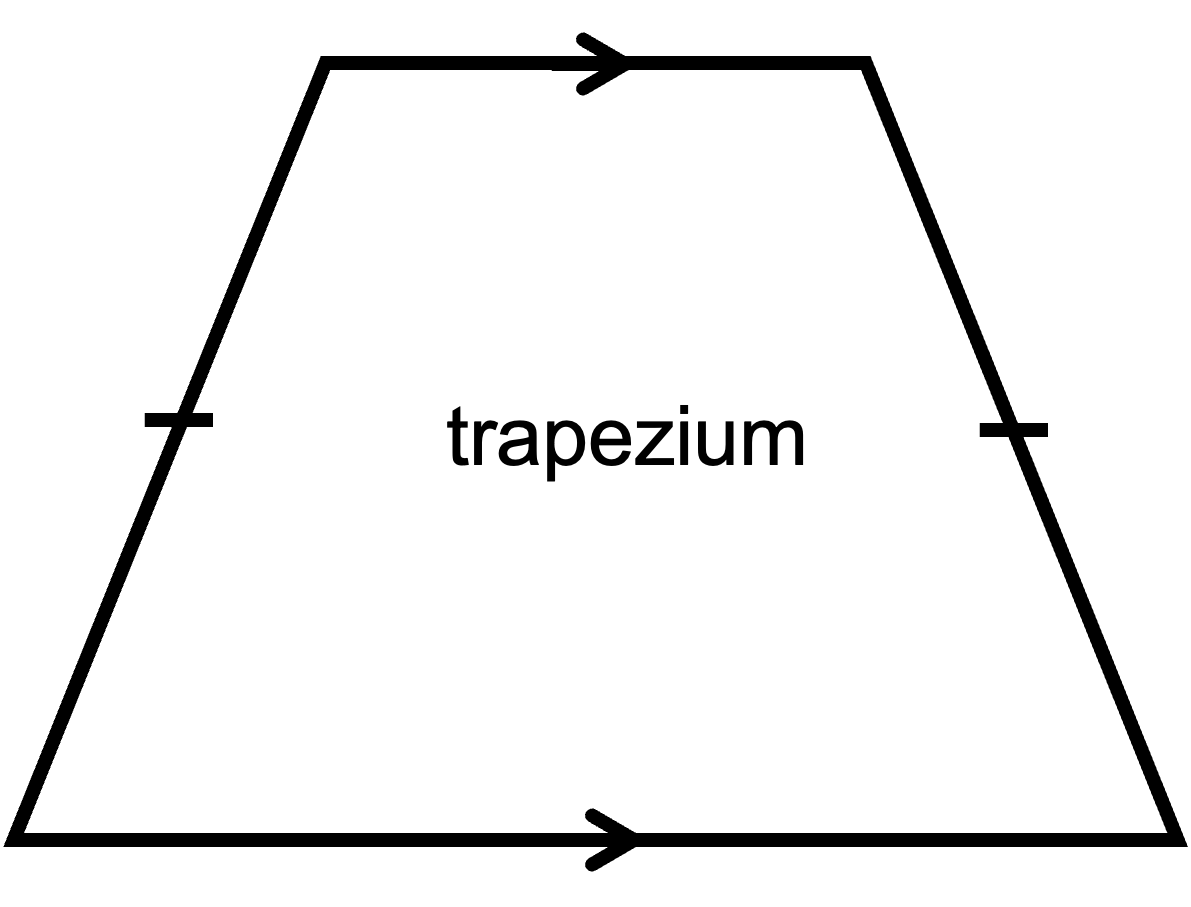
In both cases, it is best to just add up the length of all four sides to find the perimeter.
-
Area of parallelograms and trapezoids
We learnt how to find the area of rectangles (and squares) in the previous section. We can use this knowledge to help us to find the area of parallelograms and trapezoids.
For this activity, you are going to need some blank paper, a ruler, a pencil and a pair of scissors.
Part 1:
1. Draw the following rectangle on your piece of paper. Be as accurate as you can.
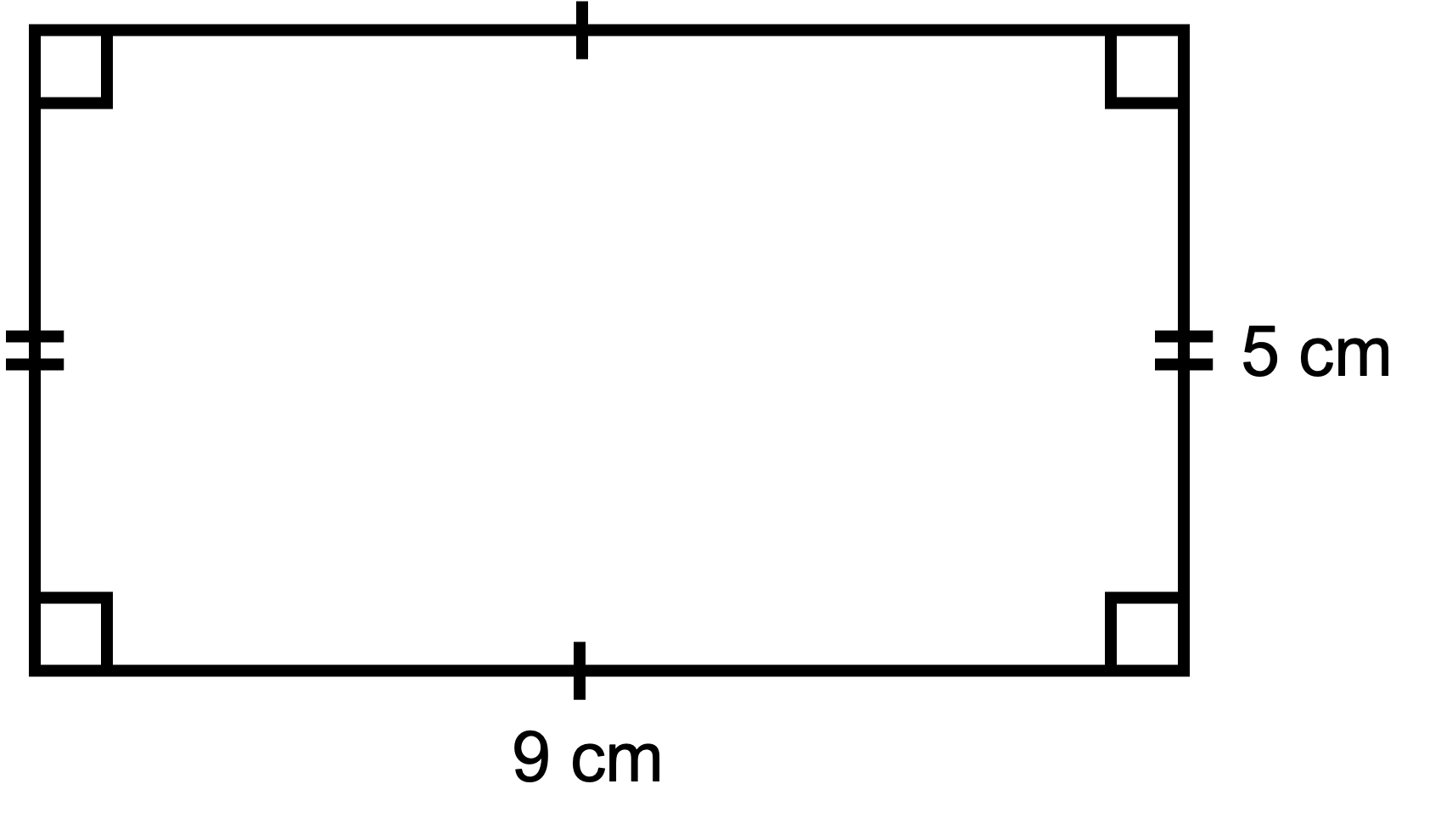
2. What is the area of this rectangle?
3. Cut your rectangle out and then cut a triangle shape off the one end as shown.
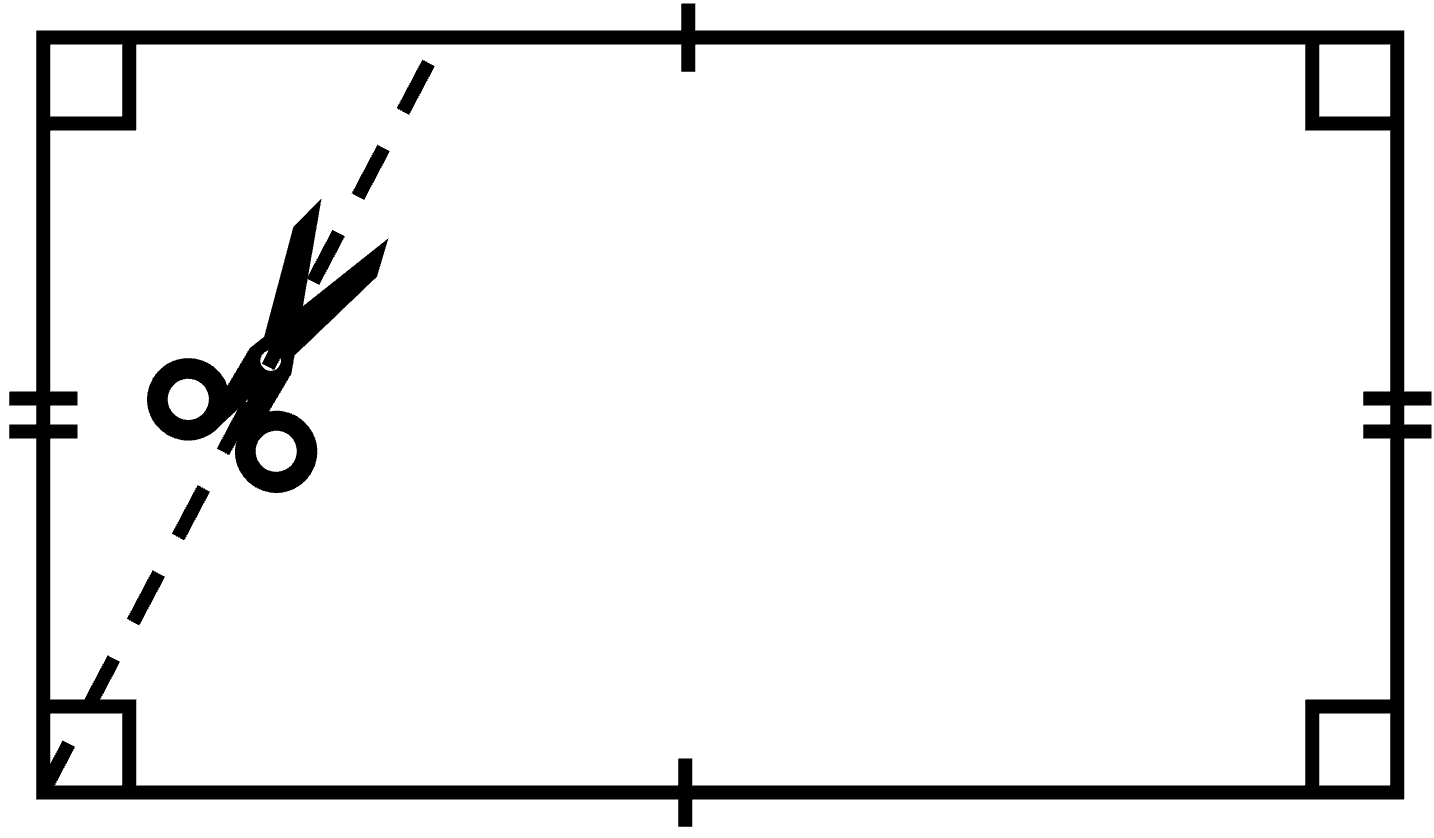
4. Move this triangle over to the other side of the shape. What kind of shape do you create?
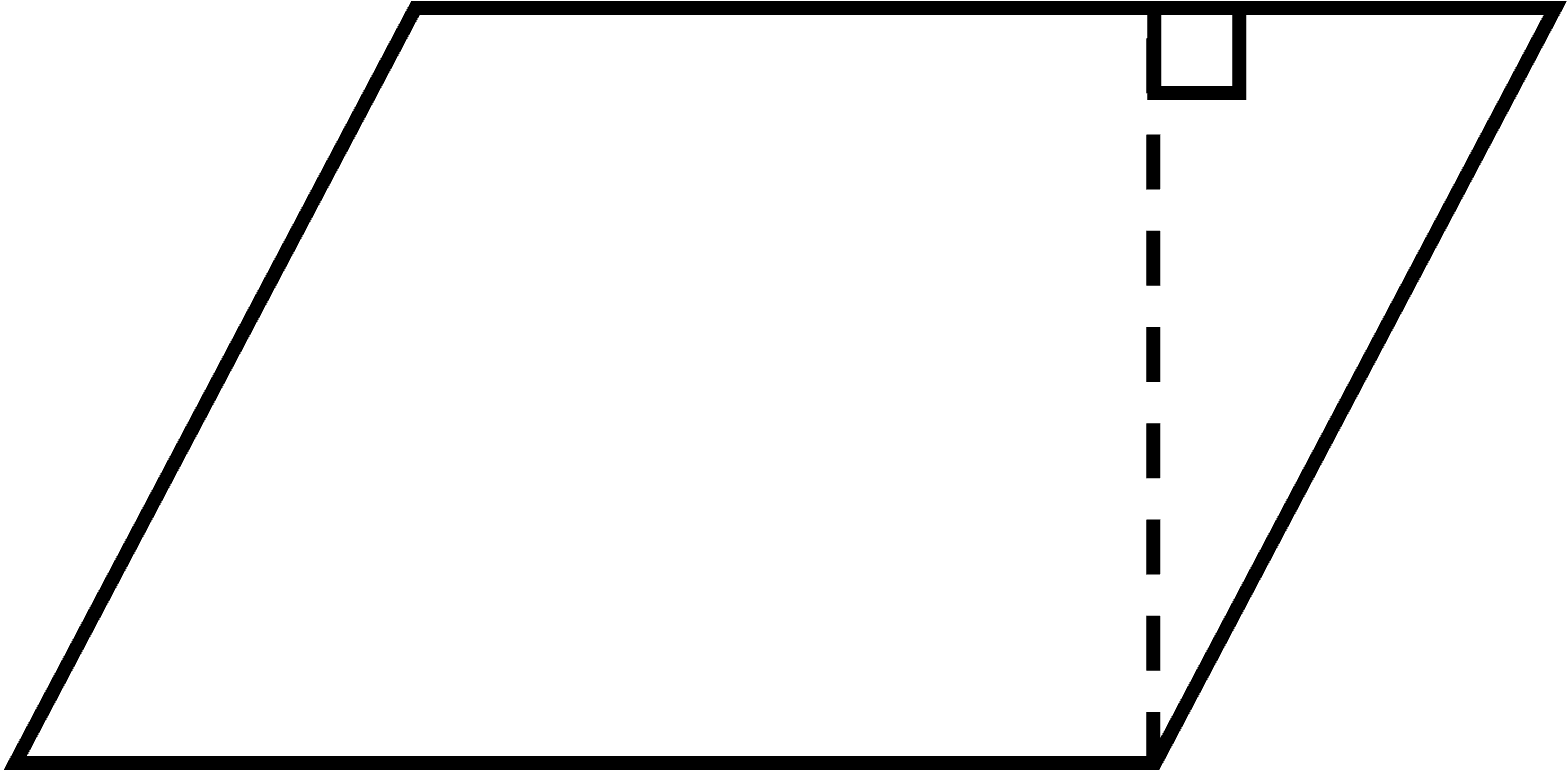
5. Is the area of this parallelogram the same as the area of the original rectangle? How do you know?
7. Will we alway be able to make a parallelogram out of a rectangle like this?
8. What can you say about how to find the area of a parallelogram?
Answer 1:
We can find the area of the original rectangle as A = b x h = 9 cm x 5 cm = 45 cm2.
The area of the parallelogram we created must be the same as the area of the original rectangle because it is made up of the same amount of paper. Therefore, the area of the new parallelogram is also 45 cm2.
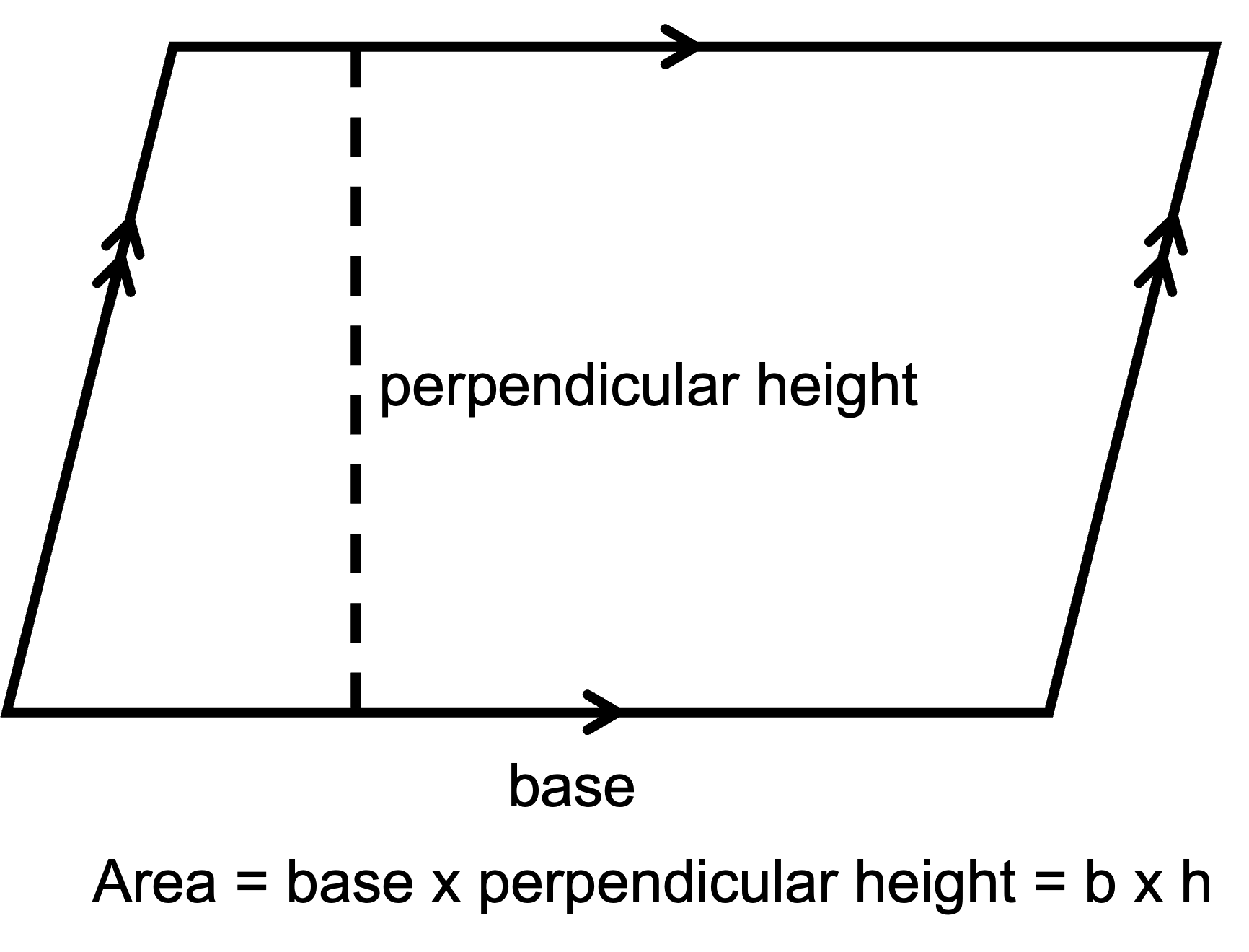
We can calculate the area of any parallelogram as A = b x h.
BUT, h must be the perpendicular height. In other words, it is the distance between the two base sides NOT the length of the other sides.
Part 2:
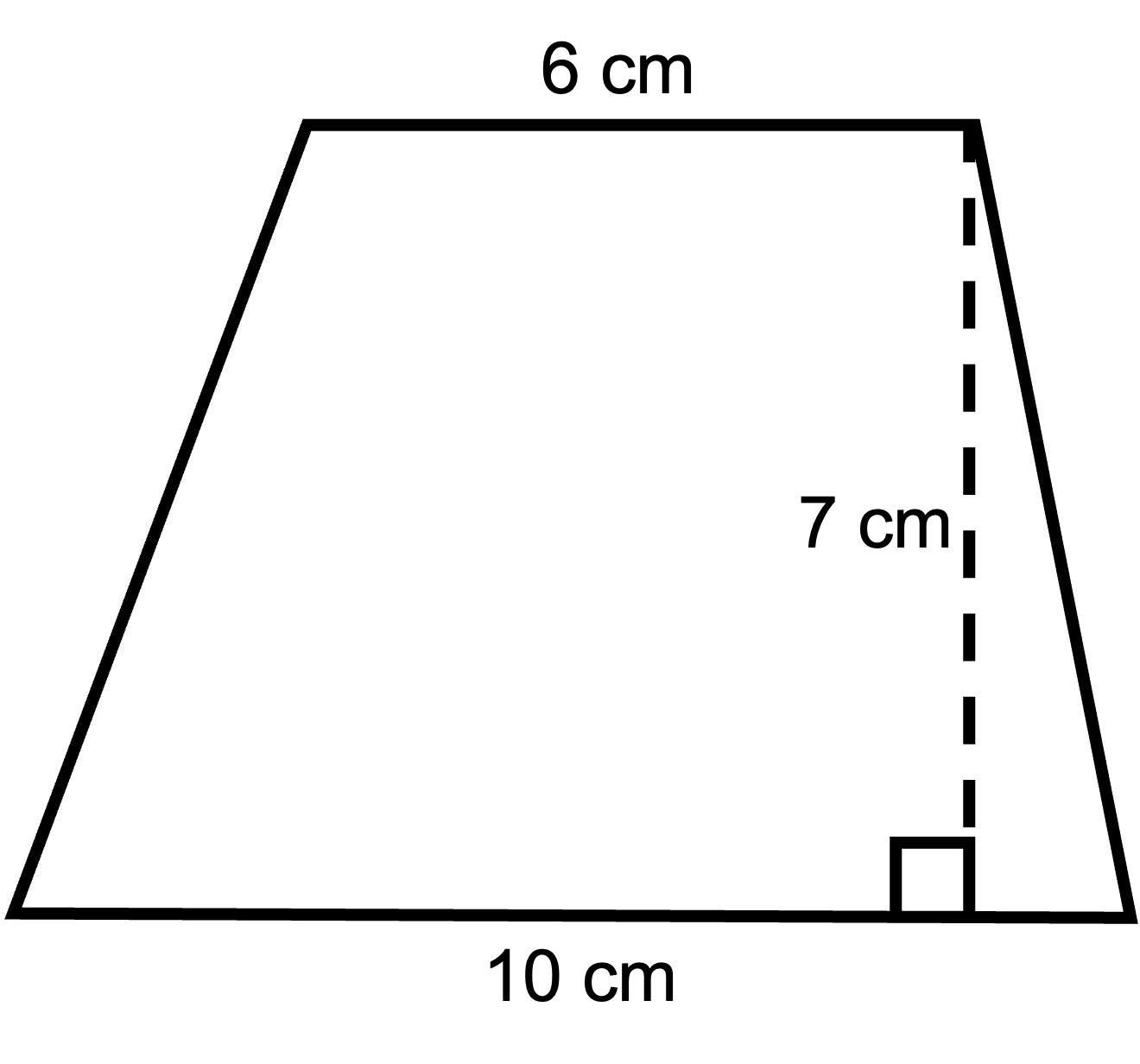
1. Draw the following trapezoid on your piece of paper. Be as accurate as you can.
2. Now cut this shape out. Use it as a stencil to cut another copy of this shape out so that you have two identical trapezoids.
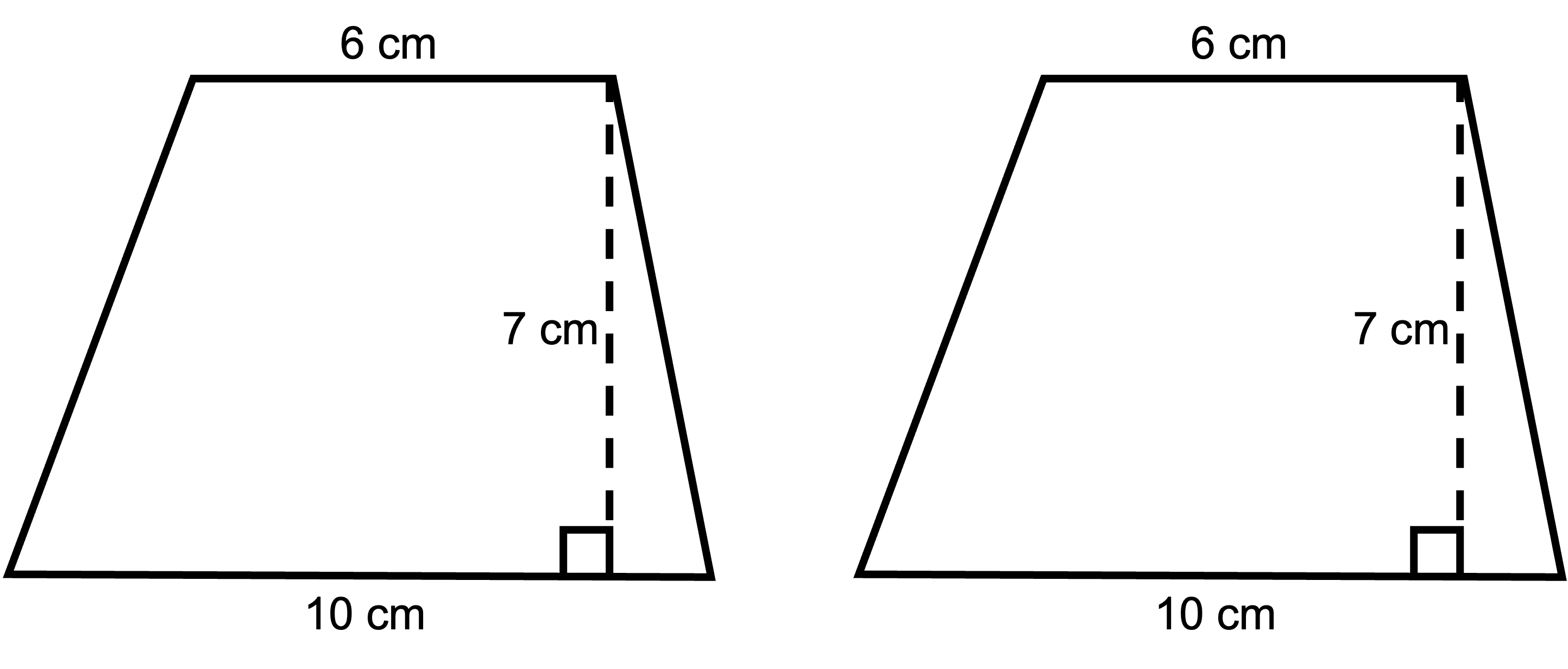
3. Arrange these trapezoids into a parallelogram.
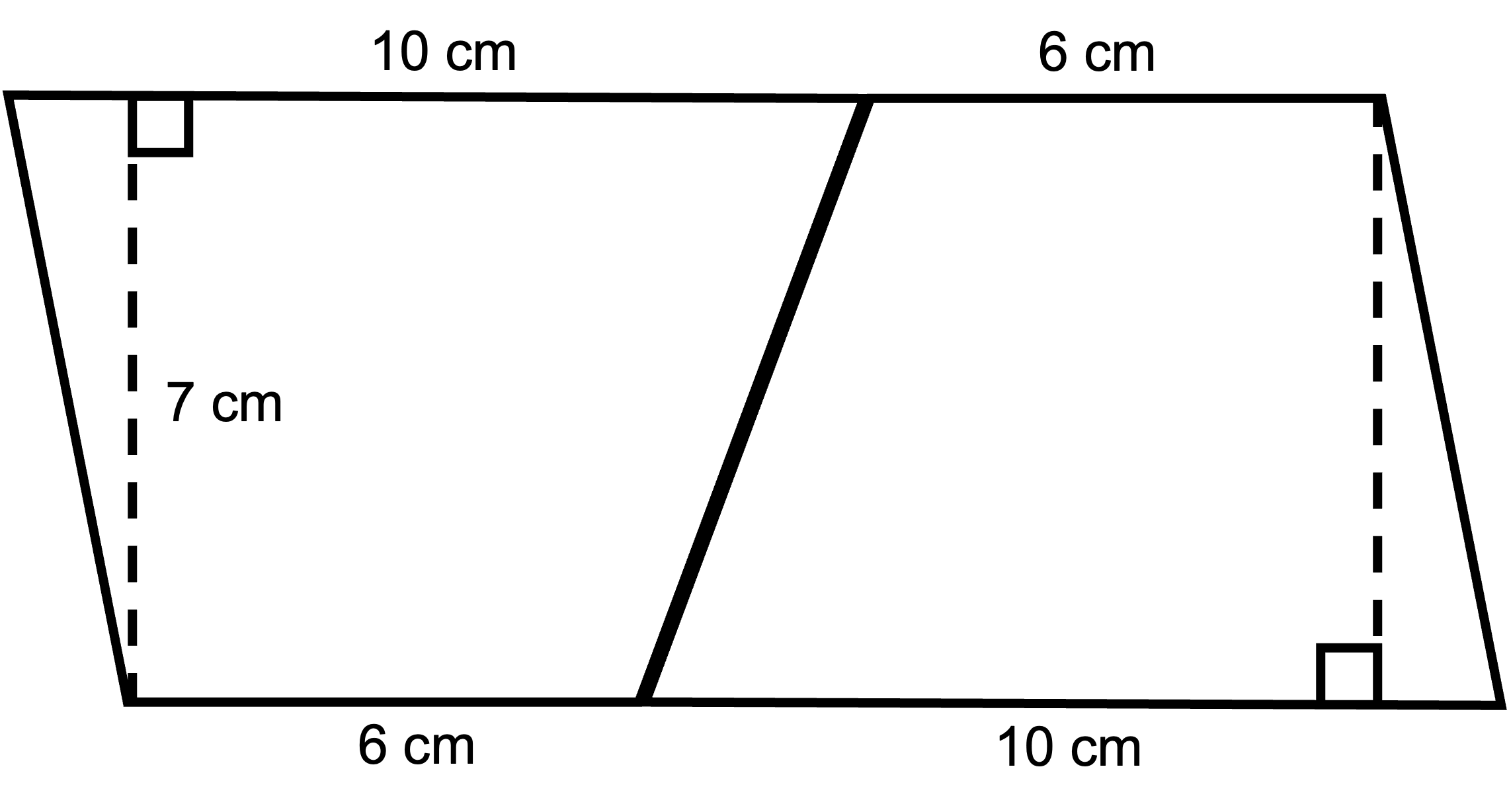
4. What is the area of this parallelogram?
5. How does the area of this parallelogram compare to the area of your original trapezoid?
6. What can you say about how to find the area of a trapezoid?
Answer 2:
The length of the base of the parallelogram you created is 10 cm + 6 cm = 16 cm. Therefore, the area of the parallelogram is A = b x h = 16 cm x 7 cm = 112 cm2.
The area of the original trapezoid is half the area of the parallelogram. But to find the area of the parallelogram we had to add the lengths of the two parallel sides of the original trapezoid.
This means that the area of a trapezoid is
\( \text{Area of trapezoid}=\frac{1}{2}\text{area of parallelogram} \)
\( \text{Area}=\frac{1}{2}\left(\text{base}_1 + \text{base}_2\right)\times \text{perpendicular height} \)
or \( A=\frac{1}{2}\left(b_1 + b_2 \right)\times h \)
-
Activity: Perimeter and area of parallelograms and trapezoids
To learn about finding the perimeter and area of parallelograms and trapezoids, work through the CK-12 FlexBook chapter called Area of Quadrilaterals.
It begins with a refresher of finding the perimeter and area of rectangles (and squares).
-
Activity: Perimeter and area of trapezoids
Get more practice finding the perimeter and area of trapezoids by working through the CK-12 FlexBook chapter called Area and Perimeter of Trapezoids.
-
Activity: Interactive challenge
Work through this interactive challenge from CK-12 to practice finding the perimeter and area of rectangles and squares.
-
